摘要:11.在区间[0,1]内任取两个实数x,y.构成一对实数对(x,y),根据下面流程图: 若开始时输入的m值为100.则根据概率学理论.从理论上来说.输出的n的值为 .
网址:http://m.1010jiajiao.com/timu_id_4402792[举报]
下列四个命题:①在区间[0,1]内任取两个实数x,y,则事件“x2+y2>1恒成立”的概率是1-
; ②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个; ③函数f(x)关于(3,0)点对称,满足f(6+x)=f(6-x),且当x∈[0,3]时函数为增函数,则f(x)在[6,9]上为减函数; ④满足A=30°,BC=1,AB=
的△ABC有两解.其中正确命题的个数为( )
| π |
| 4 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
下列四个命题:①在区间[0,1]内任取两个实数x,y,则事件“x2+y2>1恒成立”的概率是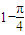 ; ②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个; ③函数f(x)关于(3,0)点对称,满足f(6+x)=f(6-x),且当x∈[0,3]时函数为增函数,则f(x)在[6,9]上为减函数; ④满足A=30°,BC=1,
; ②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个; ③函数f(x)关于(3,0)点对称,满足f(6+x)=f(6-x),且当x∈[0,3]时函数为增函数,则f(x)在[6,9]上为减函数; ④满足A=30°,BC=1,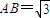 的△ABC有两解.其中正确命题的个数为( )
的△ABC有两解.其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看习题详情和答案>>
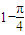 ; ②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个; ③函数f(x)关于(3,0)点对称,满足f(6+x)=f(6-x),且当x∈[0,3]时函数为增函数,则f(x)在[6,9]上为减函数; ④满足A=30°,BC=1,
; ②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个; ③函数f(x)关于(3,0)点对称,满足f(6+x)=f(6-x),且当x∈[0,3]时函数为增函数,则f(x)在[6,9]上为减函数; ④满足A=30°,BC=1,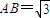 的△ABC有两解.其中正确命题的个数为( )
的△ABC有两解.其中正确命题的个数为( )A.1
B.2
C.3
D.4
查看习题详情和答案>>
下列四个命题:①在区间[0,1]内任取两个实数x,y,则事件“x2+y2>1恒成立”的概率是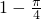 ; ②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个; ③函数f(x)关于(3,0)点对称,满足f(6+x)=f(6-x),且当x∈[0,3]时函数为增函数,则f(x)在[6,9]上为减函数; ④满足A=30°,BC=1,
; ②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个; ③函数f(x)关于(3,0)点对称,满足f(6+x)=f(6-x),且当x∈[0,3]时函数为增函数,则f(x)在[6,9]上为减函数; ④满足A=30°,BC=1,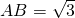 的△ABC有两解.其中正确命题的个数为
的△ABC有两解.其中正确命题的个数为
- A.1
- B.2
- C.3
- D.4
已知函数y=f(x),x∈D,如果对于定义域D内的任意实数x,对于给定的非零常数m,总存在非零常数T,恒有f(x+T)>m•f(x)成立,则称函数f(x)是D上的m级类增周期函数,周期为T.若恒有f(x+T)=m•f(x)成立,则称函数f(x)是D上的m级类周期函数,周期为T.
(1)试判断函数f(x)=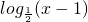 是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;
是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;
(2)已知函数f(x)=-x2+ax是[3,+∞)上的周期为1的2级类增周期函数,求实数a的取值范围;
(3)下面两个问题可以任选一个问题作答,如果你选做了两个,我们将按照问题(Ⅰ)给你记分.
(Ⅰ)已知T=1,y=f(x)是[0,+∞)上m级类周期函数,且y=f(x)是[0,+∞)上的单调递增函数,当x∈[0,1)时,f(x)=2x,求实数m的取值范围.
(Ⅱ)已知当x∈[0,4]时,函数f(x)=x2-4x,若f(x)是[0,+∞)上周期为4的m级类周期函数,且y=f(x)的值域为一个闭区间,求实数m的取值范围.
查看习题详情和答案>>
已知函数y=f(x),x∈D,如果对于定义域D内的任意实数x,对于给定的非零常数m,总存在非零常数T,恒有f(x+T)>m•f(x)成立,则称函数f(x)是D上的m级类增周期函数,周期为T.若恒有f(x+T)=m•f(x)成立,则称函数f(x)是D上的m级类周期函数,周期为T.
(1)试判断函数f(x)= 是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;
是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;
(2)已知函数f(x)=-x2+ax是[3,+∞)上的周期为1的2级类增周期函数,求实数a的取值范围;
(3)下面两个问题可以任选一个问题作答,如果你选做了两个,我们将按照问题(Ⅰ)给你记分.
(Ⅰ)已知T=1,y=f(x)是[0,+∞)上m级类周期函数,且y=f(x)是[0,+∞)上的单调递增函数,当x∈[0,1)时,f(x)=2x,求实数m的取值范围.
(Ⅱ)已知当x∈[0,4]时,函数f(x)=x2-4x,若f(x)是[0,+∞)上周期为4的m级类周期函数,且y=f(x)的值域为一个闭区间,求实数m的取值范围.
查看习题详情和答案>>
(1)试判断函数f(x)=
 是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;
是否为(3,+∞)上的周期为1的2级类增周期函数?并说明理由;(2)已知函数f(x)=-x2+ax是[3,+∞)上的周期为1的2级类增周期函数,求实数a的取值范围;
(3)下面两个问题可以任选一个问题作答,如果你选做了两个,我们将按照问题(Ⅰ)给你记分.
(Ⅰ)已知T=1,y=f(x)是[0,+∞)上m级类周期函数,且y=f(x)是[0,+∞)上的单调递增函数,当x∈[0,1)时,f(x)=2x,求实数m的取值范围.
(Ⅱ)已知当x∈[0,4]时,函数f(x)=x2-4x,若f(x)是[0,+∞)上周期为4的m级类周期函数,且y=f(x)的值域为一个闭区间,求实数m的取值范围.
查看习题详情和答案>>