摘要:解:(1)证明:定义在R上的函数对任意的. 都有成立 令 令 ∴ ∴为奇函数 知:为奇函数. ∴ 任取.且.则 ∵ ∴ ∵当时.. ∴.∴ ∴是R上的增函数. (3)解:∵.且 ∴ 由不等式.得 由(2)知:是R上的增函数 ∴ ∴不等式的解集为:
网址:http://m.1010jiajiao.com/timu_id_4398262[举报]
定义在R上的函数f(x)满足:对于任意实数a,b总有f(a+b)=f(a)•f(b),当x>0时,0<f(x)<1,且f(1)=
.
(Ⅰ)用定义法证明:函数f(x)在(-∞,+∞)上为减函数;
(Ⅱ)解关于x的不等式f(kx2-5kx+6k)•f(-x2+6x-7)>
(k∈R);
(Ⅲ)若x∈[-1,1],求证:
≥
(k∈R).
查看习题详情和答案>>
| 1 |
| 2 |
(Ⅰ)用定义法证明:函数f(x)在(-∞,+∞)上为减函数;
(Ⅱ)解关于x的不等式f(kx2-5kx+6k)•f(-x2+6x-7)>
| 1 |
| 4 |
(Ⅲ)若x∈[-1,1],求证:
| 8k+27k+1 |
| 3 |
| 6k•f(x) |
| 2 |
定义在R上的函数f(x)满足对任意x,y∈R都有f(x+y)=f(x)+f(y).当x>0,f(x)>0,
(1)求证:f(x)为奇函数;
(2)判断f(x)的单调性并证明;
(3)解不等式:f[log2(x+
+6)]+f(-3)≤0.
查看习题详情和答案>>
(1)求证:f(x)为奇函数;
(2)判断f(x)的单调性并证明;
(3)解不等式:f[log2(x+
| 1 | x |
 .
.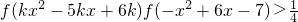 (k∈R);
(k∈R);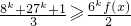 (k∈R).
(k∈R). .
. .
.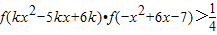 (k∈R);
(k∈R);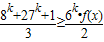 (k∈R).
(k∈R).