网址:http://m.1010jiajiao.com/timu_id_4398258[举报]
(1)求数列{an}的通项公式;
(2)设各项均不为0的数列{cn}中,满足ci•ci+1<0的正整数i的个数称作数列{cn}的变号数,令cn=1-
| a | an |
(本小题满分12分)已知函数
(I)若函数 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(II)当 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
(Ⅲ)求证:解:(1) ,其定义域为
,其定义域为 ,则
,则 令
令 ,
,
则 ,
,
当 时,
时, ;当
;当 时,
时,
 在(0,1)上单调递增,在
在(0,1)上单调递增,在 上单调递减,
上单调递减,
即当 时,函数
时,函数 取得极大值. (3分)
取得极大值. (3分)
 函数
函数 在区间
在区间 上存在极值,
上存在极值,
 ,解得
,解得 (4分)
(4分)
(2)不等式 ,即
,即
令
(6分)
令 ,则
,则 ,
,
 ,即
,即 在
在 上单调递增, (7分)
上单调递增, (7分)
 ,从而
,从而 ,故
,故 在
在 上单调递增, (7分)
上单调递增, (7分)
 (8分)
(8分)
(3)由(2)知,当 时,
时, 恒成立,即
恒成立,即 ,
,
令 ,则
,则 , (9分)
, (9分)

(10分)
以上各式相加得,

即 ,
,
即
 (12分)
(12分)
 。
。
查看习题详情和答案>>
(08年宣武区质量检一文)(14分)
已知二次函数f(x)=![]() 同时满足:
同时满足:![]() ①不等式f(x)
①不等式f(x)![]() 0的解集有且只有一个元素②在定义域内存在0
0的解集有且只有一个元素②在定义域内存在0![]() ,使得不等式
,使得不等式![]() 成立。设数列{
成立。设数列{![]() }的前n项和
}的前n项和![]() .
.
(1) 求函数f(x)的表达式;
(2) 求数列{![]() }的通项公式;
}的通项公式;
设各项均不为零的数列{![]() }中,所有满足
}中,所有满足![]() 的整数i的个数称为这个数列{
的整数i的个数称为这个数列{![]() }的变号数。令
}的变号数。令![]() (n为正整数),求数列{
(n为正整数),求数列{![]() }的变号数。
}的变号数。
 的不等式
的不等式 的解集为
的解集为 ,解关于
,解关于 ”,有如下解法:
”,有如下解法:
 ,令
,令 ,则
,则 ,
, .
. 的解集为
的解集为 ,则
,则 的解集为 .
的解集为 . 的不等式
的不等式 的解集为
的解集为 ,解关于
,解关于 ”,有如下解法:
”,有如下解法:
 ,令
,令 ,则
,则 ,
, .
. 的解集为
的解集为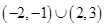 ,则
,则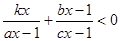 的解集为 ___________________ .
的解集为 ___________________ .