摘要：解:∵f¢ (x)＝4a0x3+3a1x2+2a2x+a3为偶函数.∴ f ¢(-x) = f ¢(x), ∴ -4a0x3 +3a1x2 -2a2x + a3 = 4a0x3+3a1x2 +2a2x + a3, ∴ 4a0x3 + 2a2x =0对一切x Î R恒成立. ∴ a0＝a2＝0.∴f (x)＝a1x3+a3x 又当x＝-时.f (x)取得极大值 ∴ 解得∴f (x)＝x3-x.f¢ (x)＝2x2-1 4分 ⑵解:设所求两点的横坐标为x1.x2 (x1 < x2).则(2x12-1)(2x22-1)＝-1 又∵x1.x2∈[-1.1].∴2x12-1∈[-1.1].2x22-1∈[-1.1] ∴2x12-1.2x22-1中有一个为1.一个为-1. ∴或 .∴所求的两点为与(-1.). ⑶证明:易知sin x∈[-1.1].cos x∈[-1.1]. 当0< x < 时.f ¢ (x) < 0,当 < x < 1时.f ¢ (x)>0. ∴f (x)在[0.]为减函数.在[.1]上为增函数. 又f (0)＝0.f ()＝- .f (1)＝-.而f (x)在[-1.1]上为奇函数. ∴f (x)在[-1.1]上最大值为.最小值为-.即 | f (x) | ≤ , ∴| f (sin x) | ≤ .| f (cos x)| ≤ . ∴| f (sin x)-f (cos x)| ≤ | f (sin x)|+| f (cos x) | ≤
网址：http://m.1010jiajiao.com/timu_id_4398255[举报]
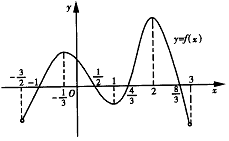
函数y＝f(x)在定义域(－
，3)内可导，其图像如图所示.记y＝f(x)的导函数为y＝f¢(x)，则不等式f¢(x)>0的解集为（ ）
A．(－
，1)∪(2，3)
B．(－1，
)∪(
，
)
C．(－，－)∪(1，2)
D．(－，－)∪(，)∪(，3)
查看习题详情和答案>>
函数y＝f(x)在定义域(－
，3)内可导，其图像如图所示.记y＝f(x)的导函数为y＝f¢(x)，
则不等式f¢(x)>0的解集为（ ）
A．(－
，1)∪(2，3) B．(－1，
)∪(
，
)
C．(－，－)∪(1，2) D．(－，－)∪(，)∪(，3)
查看习题详情和答案>>
函数y＝f（x）在定义域（－
，3）内的图像如图所示．记y＝f（x）的导函数
为y＝f¢（x），则不等式f¢（x）≤0的解集为 （ ）
A．[－
，1]∪[2，3）
B．[－1，
]∪[
，
]
C．[－，]∪[1，2）
D．（－，－ ]∪[，]∪[，3）
查看习题详情和答案>>
，3）内的图像如图所示．记y＝f（x）的导函数为y＝f¢（x），则不等式f¢（x）≤0的解集为 （ ）
，1]∪[2，3） B．[－1，
]∪[
，
]
，3）内的图像如图所示．记y＝f（x）的导函数为y＝f¢（x），则不等式f¢（x）≤0的解集为（ ）
，1]∪[2，3） 
]∪[
，
]