摘要:解:(I)设动点的坐标为.由于动点到点的距离与到直线的距离之比为.故. 2分 化简得:.这就是动点的轨迹方程. 6分 (II)设直线AB的方程为 代入.整理得 ∵直线AB过椭圆的左焦点F.∴方程有两个不等实根. 8分 记.中点. 则 ∵线段AB的中点在直线上. ∴ ∴.或 10分 当直线AB与轴垂直时.线段AB的中点F不在直线上. ∴直线AB的方程是或. 14分
网址:http://m.1010jiajiao.com/timu_id_4398059[举报]
(本小题满分12分)
已知定点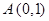 ,直线
,直线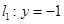 交
交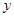 轴于点
轴于点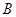 ,记过点
,记过点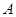 且与直线
且与直线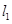 相切的圆的圆心为点
相切的圆的圆心为点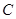 .
.
(I)求动点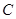 的轨迹
的轨迹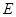 的方程;
的方程;
(Ⅱ)设倾斜角为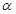 的直线
的直线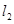 过点
过点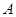 ,交轨迹
,交轨迹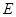 于两点
于两点
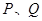 ,交直线
,交直线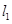 于点
于点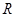 .若
.若 ,求
,求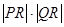 的最小值.
的最小值.
查看习题详情和答案>>
(本题满分12分)
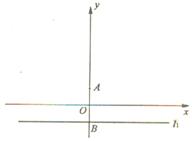
如图6,在平面直角坐标系 中,设点
中,设点 ,直线
,直线 :
: ,点
,点 在直线
在直线 上移动,
上移动, 是线段
是线段 与
与 轴的交点,
轴的交点,  .
.
(I)求动点 的轨迹的方程
的轨迹的方程 ;
;
(II)设圆 过
过 ,且圆心
,且圆心 在曲线
在曲线 上,
上, 是圆
是圆 在
在 轴上截得的弦,当
轴上截得的弦,当 运动时弦长
运动时弦长 是否为定值?请说明理由.
是否为定值?请说明理由.
(本题满分12分)
如图6,在平面直角坐标系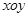 中,设点
中,设点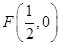 ,直线
,直线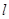 :
: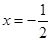 ,点
,点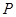 在直线
在直线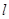 上移动,
上移动,
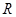 是线段
是线段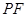 与
与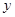 轴的交点,
轴的交点, 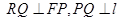 .
.
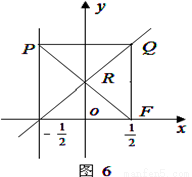
(I)求动点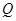 的轨迹的方程
的轨迹的方程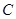 ;
;
(II)设圆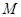 过
过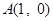 ,且圆心
,且圆心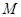 在曲线
在曲线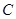 上,
上,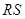 是圆
是圆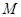 在
在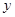 轴上截得的弦,当
轴上截得的弦,当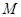 运动时弦长
运动时弦长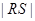 是否为定值?请说明理由.
是否为定值?请说明理由.
查看习题详情和答案>>