摘要：定理1.函数 y = f (x)的图像关于点A 对称的充要条件是 f = 2b 证明:是y = f (x)图像上任一点.∵点P的对称点P`也在y = f (x)图像上.∴ 2b-y = f 即y + f + f = 2b.必要性得证. 设点P(x0,y0)是y = f (x)图像上任一点.则y0 = f (x0) ∵ f =2b∴f (x0) + f (2a-x0) =2b.即2b-y0 = f (2a-x0) . 故点P`(2a-x0.2b-y0)也在y = f (x) 图像上.而点P与点P`关于点A 对称.充分性得征. 推论:函数 y = f (x)的图像关于原点O对称的充要条件是f = 0 定理2. 函数 y = f (x)的图像关于直线x = a对称的充要条件是 f 即f 推论:函数 y = f (x)的图像关于y轴对称的充要条件是f 定理3. ①若函数y = f (x) 图像同时关于点A 成中心对称是周期函数.且2| a-b|是其一个周期. ②若函数y = f (x) 图像同时关于直线x = a 和直线x = b成轴对称 是周期函数.且2| a-b|是其一个周期. ③若函数y = f (x)图像既关于点A 成中心对称又关于直线x =b成轴对称是周期函数.且4| a-b|是其一个周期. ①②的证明留给读者.以下给出③的证明: ∵函数y = f (x)图像既关于点A 成中心对称. ∴f =2c.用2b-x代x得: f ] =2c------(*) 又∵函数y = f (x)图像直线x =b成轴对称. ∴ f 得: f + x]-----x代x得 f [2 (a-b)+ x] = 2c-f [4得: f + x],故y = f (x)是周期函数.且4| a-b|是其一个周期.
网址：http://m.1010jiajiao.com/timu_id_4396823[举报]
设y＝f(x)是定义在R上的函数，如果存在A点，对函数y＝f(x)的图像上任意点P，P关于点A的对称点Q也在函数y＝f(x)的图像上，则称函数y＝f(x)关于点A对称，A称为函数f(x)的一个对称点．对于定义在R上的函数f(x)，可以证明点A(a，b)是f(x)图像的一个对称点的充要条件是f(a－x)＋f(a＋x)＝2b，x∈R．
(1)求函数f(x)＝x3＋3x2图像的一个对称点；
(2)函数g(x)＝ax2＋bx＋c(a≠0)的图像是否有对称点？若存在则求之，否则说明理由．
－1(x∈R)的反函数，函数g(x)的图像
的图像关于y轴对称，设F(x)=f(x)+g(x). 
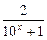－1(x∈R)的反函数，函数g(x)的图像
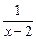的图像关于y轴对称，设F(x)=f(x)+g(x). 