摘要:解(1)由最低点为得A=2. 由x轴上相邻的两个交点之间的距离为得=.即. 由点在图像上的 故 21世纪教育网 又 (2) 当=.即时.取得最大值2,当 即时.取得最小值-1.故的值域为[-1,2] 21世纪教育网
网址:http://m.1010jiajiao.com/timu_id_4395147[举报]
已知函数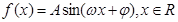 (其中
(其中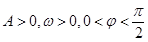 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为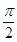 ,且图象上一个最低点为
,且图象上一个最低点为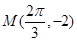 .
.
(1)求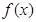 的解析式; (2)当
的解析式; (2)当 ,求
,求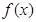 的值域.
的值域.
【解析】第一问利用三角函数的性质得到)由最低点为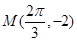 得A=2. 由x轴上相邻的两个交点之间的距离为
得A=2. 由x轴上相邻的两个交点之间的距离为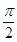 得
得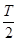 =
=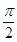 ,即
,即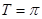 ,
,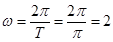 由点
由点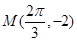 在图像上的
在图像上的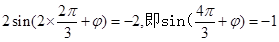
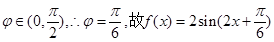
第二问中,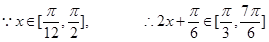

当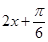 =
=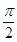 ,即
,即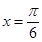 时,
时,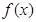 取得最大值2;当
取得最大值2;当
即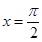 时,
时,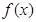 取得最小值-1,故
取得最小值-1,故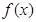 的值域为[-1,2]
的值域为[-1,2]
查看习题详情和答案>>
如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|< )图像上一个最高点坐标为(2,2
)图像上一个最高点坐标为(2,2 ),这个最高点到相邻最低点的图像与x轴交于点(5,0).
),这个最高点到相邻最低点的图像与x轴交于点(5,0).

(1)求f(x)的解析式;
(2)是否存在正整数m,使得将函数f(x)的图像向右平移m个单位后得到一个偶函数的图像?若存在,求m的最小值;若不存在,请说明理由.
查看习题详情和答案>>
如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|< )图像上一个最高点坐标为(2,2
)图像上一个最高点坐标为(2,2 ),这个最高点到相邻最低点的图像与x轴交于点(5,0).
),这个最高点到相邻最低点的图像与x轴交于点(5,0).
(1)求f(x)的解析式;
(2)是否存在正整数m,使得将函数f(x)的图像向右平移m个单位后得到一个偶函数的图像?若存在,求m的最小值;若不存在,请说明理由.
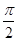 )图像上一个最高点坐标为(2,2
)图像上一个最高点坐标为(2,2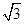 ),这个最高点到相邻最低点的图像与x轴交于点(5,0).
),这个最高点到相邻最低点的图像与x轴交于点(5,0).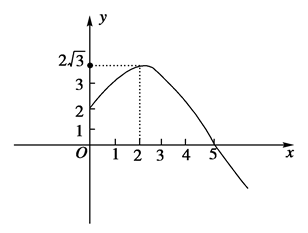
 如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|<
如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|<