摘要：2．,与型的不等式的解法 把 看作一个整体时.可化为与型的不等式来求解 即 不等式的解集为 ; 不等式的解集为
网址：http://m.1010jiajiao.com/timu_id_4393707[举报]
选做题：（从所给的A，B两题中任选一题作答，若做两题，则按第一题A给分，共5分）
A．在极坐标系（ρ，θ）（0≤θ≤2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点坐标为 ．
B．已知x，y，z∈R，有下列不等式：
（1）x2+y2+z2+3≥2（x+y+z）；（2）
≥
；
（3）|x+y|≤|x-2|+|y+2|；（4）x2+y2+z2≥xy+yz+zx．
其中一定成立的不等式的序号是 ．
查看习题详情和答案>>
A．在极坐标系（ρ，θ）（0≤θ≤2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点坐标为
B．已知x，y，z∈R，有下列不等式：
（1）x2+y2+z2+3≥2（x+y+z）；（2）
| x+y |
| 2 |
| xy |
（3）|x+y|≤|x-2|+|y+2|；（4）x2+y2+z2≥xy+yz+zx．
其中一定成立的不等式的序号是
：关于
的不等式
的解集是
；
：函数
的定义域为R。如果
的取值范围.
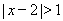
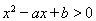
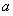
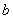
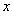
的极坐标方程为: 
,点
的极坐标为
,过点
的不等式
的解集不是空集，则实数
的取值范围是 .
的直径
,P是AB的延长线上一点,过点P作圆
,则
.
是极点，则
的面积等于_______；
的不等式
的解集是____ ____。