摘要:2.初中已学过的不等式的三条基本性质是什么?你能用汉语语言叙述这三条性质吗? ⑴. 如果a>b,那么a+c>b+c; ⑵. 如果a>b,c>0,那么 ac > bc; ⑶. 如果a>b,c<0,那么ac < bc.
网址:http://m.1010jiajiao.com/timu_id_4393704[举报]
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若
=x
,
=y
.
(1)求证:x与y的关系为y=
;
(2)设f(x)=
,定义在R上的偶函数F(x),当x∈[0,1]时F(x)=f(x),且函数F(x)图象关于直线x=1对称,求证:F(x+2)=F(x),并求x∈[2k,2k+1](k∈N)时的解析式;
(3)在(2)的条件下,不等式F(x)<-x+a在x∈[2k,2k+1](k∈N)上恒成立,求实数a的取值范围. 查看习题详情和答案>>
| OM |
| OA |
| ON |
| OB |
(1)求证:x与y的关系为y=
| x |
| x+1 |
(2)设f(x)=
| x |
| x+1 |
(3)在(2)的条件下,不等式F(x)<-x+a在x∈[2k,2k+1](k∈N)上恒成立,求实数a的取值范围. 查看习题详情和答案>>
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若 .
.
(1)求证:x与y的关系为 ;
;
(2)设 ,定义在R上的偶函数F(x),当x∈[0,1]时F(x)=f(x),且函数F(x)图象关于直线x=1对称,求证:F(x+2)=F(x),并求x∈[2k,2k+1](k∈N)时的解析式;
,定义在R上的偶函数F(x),当x∈[0,1]时F(x)=f(x),且函数F(x)图象关于直线x=1对称,求证:F(x+2)=F(x),并求x∈[2k,2k+1](k∈N)时的解析式;
(3)在(2)的条件下,不等式F(x)<-x+a在x∈[2k,2k+1](k∈N)上恒成立,求实数a的取值范围.
查看习题详情和答案>>
 .
.(1)求证:x与y的关系为
 ;
;(2)设
 ,定义在R上的偶函数F(x),当x∈[0,1]时F(x)=f(x),且函数F(x)图象关于直线x=1对称,求证:F(x+2)=F(x),并求x∈[2k,2k+1](k∈N)时的解析式;
,定义在R上的偶函数F(x),当x∈[0,1]时F(x)=f(x),且函数F(x)图象关于直线x=1对称,求证:F(x+2)=F(x),并求x∈[2k,2k+1](k∈N)时的解析式;(3)在(2)的条件下,不等式F(x)<-x+a在x∈[2k,2k+1](k∈N)上恒成立,求实数a的取值范围.
查看习题详情和答案>>
以下是某地区不同身高的未成年男性体重平均值表:
身高/cm | 60 | 70 | 80 | 90 | 100 | 110 |
体重/kg | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 |
身高cm | 120 | 130 | 140 | 150 | 160 | 170 |
体重/kg | 20.92 | 26.86 | 31.11 | 38.85 | 47.25 | 55.05 |
(1)根据表中提供的数据,能否从我们已学过的函数y=ax+b,y=alnx+b,y=a·bx中选择一种函数,使它比较近似地反映出该地区未成年男性体重y关于身高x的函数关系?试求出这个函数的解析式.
(2)若体重超过相同身高男性平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么该地区某中学一男生身高为175 cm,体重为78 kg,他的体重是否正常?
 是
是 上的增函数,且过
上的增函数,且过 和
和 两点,集合
两点,集合 ,关于
,关于 的不等式
的不等式 的解集为
的解集为 .
. 成立的实数
成立的实数 的取值范围.
的取值范围.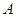 的极坐标为
的极坐标为 ,直线
,直线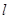 过点
过点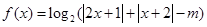 ,若关于
,若关于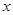 的不等式
的不等式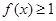 的解集为
的解集为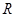 ,则
,则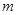 的取值范围是 .
的取值范围是 .