摘要：例3:写出求1×2×3×4×5的算法. 步骤1:先求1×2.得到结果2, 步骤2:将步骤1得到的结果2再乘以3.得到6, 步骤3:将步骤2得到的结果6再乘以4.得到结果24, 步骤4:将步骤3得到的结果24再乘以5.得到120. 例4:写出一个求整数a.b.c最大值的算法 解:S1 先假定序列中的第一个数为"最大值". S2 将序列中的下一个整数值与"最大值"比较.如果大于"最大值".这时就假定这个数为"最大值". S3 如果序列中还有其它整数.重复S2. S4 直到序列中没有可比的数为止.这时假定的"最大值"就是序列的最大值. 即 S1 max=a. S2 如果b>max.则max=b. S3 如果c>max.则max=c. S4 max就是a.b.c的最大值.
网址：http://m.1010jiajiao.com/timu_id_4393048[举报]
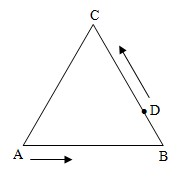例2：如图：△ABC是边长为3厘米的正三角形，D是BC边上靠近点B的三等分点，甲、乙两个质点分别从点A、D同时出发，都以1厘米/秒的速度按图示方向沿三角形的边作匀速运动，经过时间t（0≤t≤3）秒后，两质点的距离为S（t）．（1）写出函数S（t）
（2）求S（t）的最大值和最小值，并求取得最大值、最小值时相应的t的值．
对于定义域为D的函数y=f（x），如果存在区间[m，n]⊆D，同时满足：
①f（x）在[m，n]内是单调函数；
②当定义域是[m，n]时，f（x）的值域也是[m，n]．则称[m，n]是该函数的“和谐区间”．
（1）求证：函数y=g(x)=3-
不存在“和谐区间”．
（2）已知：函数y=
（a∈R，a≠0）有“和谐区间”[m，n]，当a变化时，求出n-m的最大值．
（3）易知，函数y=x是以任一区间[m，n]为它的“和谐区间”．试再举一例有“和谐区间”的函数，并写出它的一个“和谐区间”．（不需证明，但不能用本题已讨论过的y=x及形如y=
的函数为例）
查看习题详情和答案>>
①f（x）在[m，n]内是单调函数；
②当定义域是[m，n]时，f（x）的值域也是[m，n]．则称[m，n]是该函数的“和谐区间”．
（1）求证：函数y=g(x)=3-
| 5 |
| x |
（2）已知：函数y=
| (a2+a)x-1 |
| a2x |
（3）易知，函数y=x是以任一区间[m，n]为它的“和谐区间”．试再举一例有“和谐区间”的函数，并写出它的一个“和谐区间”．（不需证明，但不能用本题已讨论过的y=x及形如y=
| bx+c |
| ax |
（2011•西城区一模）将1，2，3，…，n这n个数随机排成一列，得到的一列数a1，a2，…，an称为1，2，3，…，n的一个排列；定义τ（a1，a2，…，an）=|a1-a2|+|a2-a3|+…|an-1-an|为排列a1，a2，…，an的波动强度．
（Ⅰ）当n=3时，写出排列a1，a2，a3的所有可能情况及所对应的波动强度；
（Ⅱ）当n=10时，求τ（a1，a2，…，a10）的最大值，并指出所对应的一个排列；
（Ⅲ）当n=10时，在一个排列中交换相邻两数的位置称为一次调整，若要求每次调整时波动强度不增加，问对任意排列a1，a2，…，a10，是否一定可以经过有限次调整使其波动强度降为9；若可以，给出调整方案，若不可以，请给出反例并加以说明．
查看习题详情和答案>>
（Ⅰ）当n=3时，写出排列a1，a2，a3的所有可能情况及所对应的波动强度；
（Ⅱ）当n=10时，求τ（a1，a2，…，a10）的最大值，并指出所对应的一个排列；
（Ⅲ）当n=10时，在一个排列中交换相邻两数的位置称为一次调整，若要求每次调整时波动强度不增加，问对任意排列a1，a2，…，a10，是否一定可以经过有限次调整使其波动强度降为9；若可以，给出调整方案，若不可以，请给出反例并加以说明．
如图有三根针和套在一根针上的n（n∈N*）个金属片．按下列规则，把金属片从一根针上全部移到另一根针上．
1．每次只能移动1个金属片；
2．较大的金属片不能放在较小的金属片上面．
现用an表示把n个金属片从中间的针移到右边的针上所至少需要移动的次数，请回答下列问题：
（1）写出a1，a2，a3，并求出an；
（2）记bn=an+1，求和Sn=
bibj（i，j∈N*）；（其中
bibj表示所有的积bibj（1≤i≤j≤n）的和．例：
bibj=
+b1b2+
=
[（b1+b2）2+（
+
）]
（3）证明：
≤
+
+…+
＜
（n∈N*）
查看习题详情和答案>>
1．每次只能移动1个金属片；
2．较大的金属片不能放在较小的金属片上面．
现用an表示把n个金属片从中间的针移到右边的针上所至少需要移动的次数，请回答下列问题：
（1）写出a1，a2，a3，并求出an；
（2）记bn=an+1，求和Sn=
 |
| 1≤i≤j≤n |
|
| 1≤i≤j≤n |
|
| 1≤i≤j≤2 |
| b | 2 1 |
| b | 2 2 |
| 1 |
| 2 |
| b | 2 1 |
| b | 2 2 |
（3）证明：
| 1 |
| 7 |
| S1 |
| S2 |
| S1S3 |
| S2S4 |
| S1S3…S2n-1 |
| S2S4…S2n |
| 4 |
| 21 |