摘要：1．由方程研究曲线.特别是圆锥曲线的几何性质问题常化为等式解决.要加强等价转化思想的训练,
网址：http://m.1010jiajiao.com/timu_id_4393031[举报]
（2012•奉贤区二模）平面内一动点P（x，y）到两定点F1（-1，0），F2（1，0）的距离之积等于1．
（1）求动点P（x，y）的轨迹C方程，用y2=f（x）形式表示；
（2）类似高二第二学期教材（12.4椭圆的性质、12.6双曲线的性质、12.8抛物线的性质）中研究曲线的方法请你研究轨迹C的性质，请直接写出答案；
（3）求△PF1F2周长的取值范围．
查看习题详情和答案>>
（1）求动点P（x，y）的轨迹C方程，用y2=f（x）形式表示；
（2）类似高二第二学期教材（12.4椭圆的性质、12.6双曲线的性质、12.8抛物线的性质）中研究曲线的方法请你研究轨迹C的性质，请直接写出答案；
（3）求△PF1F2周长的取值范围．
（2011•宁德模拟）由方程2x|x|-y=1所确定的x，y的函数关系记为y=f（x）．给出如下结论：
①f（x）是R上的单调递增函数；
②对于任意x∈R，f（x）+f（-x）=-2恒成立；
③存在x0∈（-1，0），使得过点A（1，f（1）），B（x0，f（x0））的直线与曲线f（x）恰有两个公共点．
其中正确的结论为
查看习题详情和答案>>
①f（x）是R上的单调递增函数；
②对于任意x∈R，f（x）+f（-x）=-2恒成立；
③存在x0∈（-1，0），使得过点A（1，f（1）），B（x0，f（x0））的直线与曲线f（x）恰有两个公共点．
其中正确的结论为
①②③
①②③
（写出所有正确结论的序号）．由方程
所确定的
的函数关系记为
.给出如下结论：
① 
是
上的单调递增函数；
②对于任意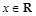
，
恒成立；
③存在
，使得过点
，
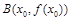的直线与曲线恰有两个公共点．
其中正确的结论为 (写出所有正确结论的序号) ．
查看习题详情和答案>>
所确定的
的函数关系记为
.给出如下结论：
是
上的单调递增函数； 
，
恒成立；
，使得过点
，
的直线与曲线