摘要：解:(1)f(2)=3.f(-2)=7 由于f(-2)≠f(2).f(-2)≠-f(2) 故f(x)既不是奇函数.也不是偶函数 (2)f(x)= 由于f(x)在［2.+∞)上的最小值为f内的最小值为. 故函数f(x)在内的最小值为. 评述:因为奇偶函数问题要紧紧抓住“任取 “都有 这两个关键词.f(-x)与f(x)要同时有意义.f(x)与f(-x)要么相等.要么互为相反数.而要讨论非奇非偶只要说明不满足上述两点之一即可.另外.也可以借助分段函数的草图.帮助分析.然后用代数方法来回答.
网址：http://m.1010jiajiao.com/timu_id_4392391[举报]
若函数f(x)=
(a∈R)是R上的奇函数
（1）求a的值，并利用定义证明函数f（x）在R上单调递增；
（2）解不等式：f(-2)+f(log
(2x))≥0．
查看习题详情和答案>>
| a•2x-2 |
| 1+2x |
（1）求a的值，并利用定义证明函数f（x）在R上单调递增；
（2）解不等式：f(-2)+f(log
| 1 |
| 2 |
已知函数f（x）=-x2+4，设函数F(x)=
．
（1）求F（x）表达式；
（2）解不等式1≤F（x）≤2；
（3）设mn＜0，m+n＞0，判断F（m）+F（n）能否小于0？ 查看习题详情和答案>>
|
（1）求F（x）表达式；
（2）解不等式1≤F（x）≤2；
（3）设mn＜0，m+n＞0，判断F（m）+F（n）能否小于0？ 查看习题详情和答案>>
解：：因为
，所以f(1)f(2)<0，因此f(x)在区间（1，2）上存在零点，又因为y=
与y=-
在（0，+
）上都是增函数，因此
在（0，+）上是增函数，所以零点个数只有一个方法2：把函数的零点个数个数问题转化为判断方程
解的个数问题，近而转化成判断
与
交点个数问题，在坐标系中画出图形
由图看出显然一个交点，因此函数的零点个数只有一个
袋中有50个大小相同的号牌，其中标着0号的有5个，标着n号的有n个（n=1,2,…9）,现从袋中任取一球，求所取号码的分布列，以及取得号码为偶数的概率.
查看习题详情和答案>>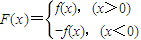
x∈R,x2-x+1＞0 ②
x∈R，使x2-x+1≤0 ③
a∈R，使f（x）=x2-ax在（-∞，0］为增函数?④至少有一个实数a的值，使ax2+1=0有解
．