摘要:对映射有两个关键点:一是有象.二是象惟一.缺一不可, 对函数三要素及其之间的关系给以深刻理解.这是处理函数问题的关键, 理解函数和映射的关系.函数式和方程式的关系.
网址:http://m.1010jiajiao.com/timu_id_4389789[举报]
定义在R上的函数y=f(x)满足:对任意的x,y∈R都有f(x)+f(y)=f(
)成立,f(1)=1,且当x>0时,f(x)>0.
(1)求f(-1)的值,并判断y=f(x)的奇偶性;
(2)证明:y=f(x)在(0,+∞)上的单调递增;
(3)若关于x的方程2f(x)=f(
)在(2,+∞)上有两个不同的实根,求实数a的取值范围.
查看习题详情和答案>>
| x2+y2 |
(1)求f(-1)的值,并判断y=f(x)的奇偶性;
(2)证明:y=f(x)在(0,+∞)上的单调递增;
(3)若关于x的方程2f(x)=f(
| a(x-1) |
| x+1 |
设函数f(x)=x|x|+bx+c(b,c∈R),则下列命题中正确的是( )
| A、“b≥0”是“函数y=f(x)在R上单调递增”的必要非充分条件 | ||
| B、“b<0,c<0”是“方程f(x)=0有两个负根”的充分非必要条件 | ||
| C、“c=0”是“函数y=f(x)为奇函数”的充要条件 | ||
D、“c>0”是“不等式f(x)≥( 2
|
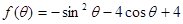 ,
,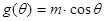
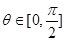 ,若
,若 恒成立,求m取值范围;
恒成立,求m取值范围;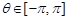 ,
, 有两个不等实根,求m的取值范围.
有两个不等实根,求m的取值范围.