摘要：问题1．解下列不等式: , , , 问题2.①二次不等式的解集是.则的值是 ②已知不等式的解集为.则不等式 的解集为 问题3． 已知. 如果对一切.恒成立.求实数的取值范围, 如果对.恒成立.求实数的取值范围． 问题4．解关于的不等式:≥ [机动]已知二次函数的图象过点.问是否存在 常数...使不等式≤≤对一切都成立?
网址：http://m.1010jiajiao.com/timu_id_4389658[举报]
已知二次函数f（x）=x2+x的定义域D 恰是不等式 f（-x）+f（x）≤2|x|的解集，其值域为A．函数 g(x)=x3-3tx+
t的定义域为[0，1]，值域为B．
（1）求f （x） 的定义域D和值域 A；
（2）（理） 试用函数单调性的定义解决下列问题：若存在实数x0∈（0，1），使得函数 g(x)=x3-3tx+
t在[0，x0]上单调递减，在[x0，1]上单调递增，求实数t的取值范围并用t表示x0．
（3）（理） 是否存在实数t，使得A⊆B成立？若存在，求实数t 的取值范围；若不存在，请说明理由．
（4）（文） 是否存在负实数t，使得A⊆B成立？若存在，求负实数t 的取值范围；若不存在，请说明理由．
（5）（文） 若函数g(x)=x3-3tx+
t在定义域[0，1]上单调递减，求实数t的取值范围．
查看习题详情和答案>>
| 1 |
| 2 |
（1）求f （x） 的定义域D和值域 A；
（2）（理） 试用函数单调性的定义解决下列问题：若存在实数x0∈（0，1），使得函数 g(x)=x3-3tx+
| 1 |
| 2 |
（3）（理） 是否存在实数t，使得A⊆B成立？若存在，求实数t 的取值范围；若不存在，请说明理由．
（4）（文） 是否存在负实数t，使得A⊆B成立？若存在，求负实数t 的取值范围；若不存在，请说明理由．
（5）（文） 若函数g(x)=x3-3tx+
| 1 |
| 2 |
已知二次函数f（x）=x2+x的定义域D 恰是不等式 f（-x）+f（x）≤2|x|的解集，其值域为A．函数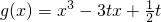 
的定义域为[0，1]，值域为B．
（1）求f （x） 的定义域D和值域 A；
（2）（理） 试用函数单调性的定义解决下列问题：若存在实数x0∈（0，1），使得函数 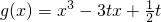在[0，x0]上单调递减，在[x0，1]上单调递增，求实数t的取值范围并用t表示x0．
（3）（理） 是否存在实数t，使得A⊆B成立？若存在，求实数t 的取值范围；若不存在，请说明理由．
（4）（文） 是否存在负实数t，使得A⊆B成立？若存在，求负实数t 的取值范围；若不存在，请说明理由．
（5）（文） 若函数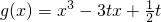在定义域[0，1]上单调递减，求实数t的取值范围．
查看习题详情和答案>>
某校初二年级全体320名学生在电脑培训前后分别参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考分等级．所绘制的统计图如图所示．
试结合图示信息回答下列问题：
(1)这32名学生培训前考分的中位数所在的等级是______，培训后考分的中位数所在的等级是______．
(2)这32名学生经过培训，考分等级“不合格”的百分比由_______下降到_______．
(3)估计该校整个初二年级中，培训后考分等级为“合格”与“优秀”的学生共有______名．
(4)你认为上述估计合理吗？理由是什么？
答：_____________________________；
理由是___________________________________．
查看习题详情和答案>>某校初二年级全体
320名学生在电脑培训前后分别参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考分等级．所绘制的统计图如图所示．
试结合图示信息回答下列问题：
(1)
这32名学生培训前考分的中位数所在的等级是______，培训后考分的中位数所在的等级是______．(2)
这32名学生经过培训，考分等级“不合格”的百分比由_______下降到_______．(3)
估计该校整个初二年级中，培训后考分等级为“合格”与“优秀”的学生共有______名．(4)
你认为上述估计合理吗？理由是什么？答：
_____________________________；理由是
___________________________________． 查看习题详情和答案>>