摘要:问题1. 已知函数. 用“五点法 画出它的图象,求它的振幅.周期和初相, 说明该函数的图象可由的图象经过怎样的变换而得到. 问题2.(海南)函数在区的简图是 (天津文)函数 的部分图象如图所示.则函数表达式为 已知函数() 的一段图象如下图所示.求该函数的解析式. 问题3.将函数的周期扩大到原来的倍.再将函数图象左移.得到图象对应解析式是 (山东文)要得到函数的图象.只需将函数 的图象 向右平移个单位,向右平移个单位, 向左平移个单位,向左平移个单位 (山东)为了得到函数的图象.可以将函数的图象 向右平移个单位长度 向右平移个单位长度 向左平移个单位长度 向左平移个单位长度 问题4.(福建)已知函数的最小正周期为.则 该函数的图象 关于点对称 关于直线对称 关于点对称 .关于直线对称 (山东)已知函数.则下列判断正确的是 此函数的最小正周期为.其图象的一个对称中心是 此函数的最小正周期为.其图象的一个对称中心是 此函数的最小正周期为.其图象的一个对称中心是 此函数的最小正周期为.其图象的一个对称中心是 问题5.(陕西)设函数.其中向量...且的图象经过点.(Ⅰ)求实数的值,(Ⅱ)求函数的最小值及此时值的集合.
网址:http://m.1010jiajiao.com/timu_id_4389559[举报]
问题1:已知函数f(x)=
,则f(
)+f(
)+…+f(
)+f(1)+f(2)+…+f(9)+f(10)=
.
我们若把每一个函数值计算出,再求和,对函数值个数较少时是常用方法,但函数值个数较多时,运算就较繁锁.观察和式,我们发现f(
)+f(2)、…、f(
)+f(9)、f(
)+f(10)可一般表示为f(
)+f(x)=
+
=
+
=
=1为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
问题2:已知函数f(x)=
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
查看习题详情和答案>>
| x |
| 1+x |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
我们若把每一个函数值计算出,再求和,对函数值个数较少时是常用方法,但函数值个数较多时,运算就较繁锁.观察和式,我们发现f(
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| x |
| ||
1+
|
| x |
| 1+x |
| 1 |
| 1+x |
| x |
| 1+x |
| 1+x |
| 1+x |
问题2:已知函数f(x)=
| 1 | ||
2x+
|
问题1:已知函数 ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______.
我们若把每一个函数值计算出,再求和,对函数值个数较少时是常用方法,但函数值个数较多时,运算就较繁锁.观察和式,我们发现 、…、
、…、 、
、 可一般表示为
可一般表示为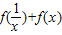 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
问题2:已知函数 ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
查看习题详情和答案>>
 ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______.我们若把每一个函数值计算出,再求和,对函数值个数较少时是常用方法,但函数值个数较多时,运算就较繁锁.观察和式,我们发现
 、…、
、…、 、
、 可一般表示为
可一般表示为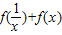 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:问题2:已知函数
 ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.查看习题详情和答案>>
问题1:已知函数f(x)=
,则f(
)+f(
)+…+f(
)+f(1)+f(2)+…+f(9)+f(10)=______.
我们若把每一个函数值计算出,再求和,对函数值个数较少时是常用方法,但函数值个数较多时,运算就较繁锁.观察和式,我们发现f(
)+f(2)、…、f(
)+f(9)、f(
)+f(10)可一般表示为f(
)+f(x)=
+
=
+
=
=1为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
问题2:已知函数f(x)=
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
查看习题详情和答案>>
| x |
| 1+x |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 2 |
我们若把每一个函数值计算出,再求和,对函数值个数较少时是常用方法,但函数值个数较多时,运算就较繁锁.观察和式,我们发现f(
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| x |
| ||
1+
|
| x |
| 1+x |
| 1 |
| 1+x |
| x |
| 1+x |
| 1+x |
| 1+x |
问题2:已知函数f(x)=
| 1 | ||
2x+
|
问题1:已知函数 ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______.
我们若把每一个函数值计算出,再求和,对函数值个数较少时是常用方法,但函数值个数较多时,运算就较繁锁.观察和式,我们发现 、…、
、…、 、
、 可一般表示为
可一般表示为 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
问题2:已知函数 ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
查看习题详情和答案>>
 ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______.我们若把每一个函数值计算出,再求和,对函数值个数较少时是常用方法,但函数值个数较多时,运算就较繁锁.观察和式,我们发现
 、…、
、…、 、
、 可一般表示为
可一般表示为 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:问题2:已知函数
 ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.查看习题详情和答案>>
(1)已知函数f(x)=ax-x(a>1).
①若f(3)<0,试求a的取值范围;
②写出一组数a,x0(x0≠3,保留4位有效数字),使得f(x0)<0成立;
(2)在曲线y=x-
上存在两个不同点关于直线y=x对称,求出其坐标;若曲线y=x+
(p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围;
(3)当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并取a=
及a=
加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间(0,
]上单调递减,在区间[
,1)上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
查看习题详情和答案>>
①若f(3)<0,试求a的取值范围;
②写出一组数a,x0(x0≠3,保留4位有效数字),使得f(x0)<0成立;
(2)在曲线y=x-
| 2 |
| x |
| p |
| x |
(3)当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并取a=
| 1 |
| 16 |
| ||
| 2 |
| 1 |
| e |
| 1 |
| e |