摘要：寻求所求结论中的角与已知条件中的角的关系.把握式子的变形方向.准确运用公式, 三角变换主要体现在:函数名称的变换.角的变换.的变换.和积的变换.幂的变换等方面, 掌握基本技巧:切割化弦.异名化同名.异角化同角等, 应注意的几点: 熟悉公式的正用.逆用.还要熟练掌握公式的变形应用. 注意拆角.凑角技巧.如.等. 注意倍角的相对性.如是的倍角. 要时时注意角的范围的讨论.
网址：http://m.1010jiajiao.com/timu_id_4389531[举报]
如图，图（1）是一个正方体的表面展开图，MN和PQ是两条面对角线．
（1）请在图（2）的正方体中画出MN、PQ；并求此时MN与PQ所成角的大小；
（2）求四面体MNPQ的体积与正方体的体积之比．（说明：求角与体积时，若需画辅助图，请分别画在图（3）、（4）中）
查看习题详情和答案>>
（1）请在图（2）的正方体中画出MN、PQ；并求此时MN与PQ所成角的大小；
（2）求四面体MNPQ的体积与正方体的体积之比．（说明：求角与体积时，若需画辅助图，请分别画在图（3）、（4）中）
如图所示，矩形ABCD的边AB=a，BC=2，PA⊥平面ABCD，PA=2，现有数据：①a=
| ||
| 2 |
| 3 |
（1）当在BC边上存在点Q，使PQ⊥QD时，a可能取所给数据中的哪些值，请说明理由；
（2）在满足（1）的条件下，a取所给数据中的最大值时，求直线PQ与平面ADP所成角的正切值；
（3）记满足（1）的条件下的Q点为Qn（n=1，2，3，…），若a取所给数据的最小值时，这样的点Qn有几个，试求二面角Qn-PA-Qn+1的大小．
在平面直角坐标系xOy中，已知⊙C1：（x+3）2+（y-1）2=4和⊙C2：（x-5）2+（y-1）2=4（1）若直线l过点O（0，0），且被⊙C1截得的弦长为2
| 3 |
（2）设P为平面上的点，满足：过点P的任意互相垂直的直线l1和l2，只要l1和l2与⊙C1和⊙C2分别相交，必有直线l1被⊙C1截得的弦长与直线l2被⊙C2截得的弦长相等，试求所有满足条件的点P的坐标；
（3）将（2）的直线l1和l2互相垂直改为直线l1和l2所成的角为60°，其余条件不变，直接写出所有这样的点P的坐标．（直线与直线所成的角与两条异面直线所成的角类似，只取较小的角度．）
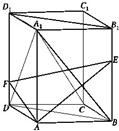如图，在长方体ABCD-A1B1C1D1中，点E、F分别BB1、DD1上，且AE⊥A1B，AF⊥A1D．
（2005•静安区一模）已知正方体ABCD-A1B1C1D1的棱长为2，点E、F分别在底面正方形的边AB、BC上，且