摘要：问题1．(山东)已知定义在上的奇函数满足.则的值为 问题2．(上海) 设的最小正周期且为偶函数, 它在区间上的图象如右图所示的线段,则在区间上, 已知函数是周期为的函数.当时.. 当 时.的解析式是 是定义在上的以为周期的函数.对.用表示区间. 已知当时..求在上的解析式. 问题3．(福建)定义在上的函数满足.当时. .则 , , (天津文) 设是定义在上以为周期的函数.在内单调递减. 且的图像关于直线对称.则下面正确的结论是 问题4．定义在上的函数.对任意.有.且.求证:,判断的奇偶性, 若存在非零常数,使.①证明对任意都有成立, ②函数是不是周期函数.为什么? 问题5．(全国)设是定义在上的偶函数.其图象关于直线对称.对任 意的.都有. 设.求.,证明:是周期函数. 记.求.
网址：http://m.1010jiajiao.com/timu_id_4389442[举报]
（2009•金山区二模）设函数f（x）=x2+x．（1）解不等式：f（x）＜0；（2）请先阅读下列材料，然后回答问题．
材料：已知函数g（x）=-
，问函数g（x）是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，说明理由．一个同学给出了如下解答：
解：令u=-f（x）=-x2-x，则u=-（x+
）2+
，
当x=-
时，u有最大值，umax=
，显然u没有最小值，
∴当x=-
时，g（x）有最小值4，没有最大值．
请回答：上述解答是否正确？若不正确，请给出正确的解答；
（3）设an=
，请提出此问题的一个结论，例如：求通项an．并给出正确解答．
注意：第（3）题中所提问题单独给分，．解答也单独给分．本题按照所提问题的难度分层给分，解答也相应给分，如果同时提出两个问题，则就高不就低，解答也相同处理．
查看习题详情和答案>>
材料：已知函数g（x）=-
| 1 |
| f(x) |
解：令u=-f（x）=-x2-x，则u=-（x+
| 1 |
| 2 |
| 1 |
| 4 |
当x=-
| 1 |
| 2 |
| 1 |
| 4 |
∴当x=-
| 1 |
| 2 |
请回答：上述解答是否正确？若不正确，请给出正确的解答；
（3）设an=
| f(n) |
| 2n-1 |
注意：第（3）题中所提问题单独给分，．解答也单独给分．本题按照所提问题的难度分层给分，解答也相应给分，如果同时提出两个问题，则就高不就低，解答也相同处理．
（2009•金山区二模）（1）设u、v为实数，证明：u2+v2≥| (u+v)2 |
| 2 |
材料：已知△LMN内接于边长为1的正三角形ABC，求证：△LMN中至少有一边的长不小于
| 1 |
| 2 |
证明：线段AN、AL、BL、BM、CM、CN的长分别设为a1、a2、b1、b2、c1、c2，设LN、LM、MN的长为x、y、z，
x2=a12+a22-2a1a2cos60°=a12+a22-a1a2
同理：y2=b12+b22-b1b2，z2=c12+c22-c1c2，
x2+y2+z2=a12+a22+b12+b22+c12+c22-a1a2-b1b2-c1c2
…
请利用（1）的结论，把证明过程补充完整；
（3）已知n边形A1′A2′A3′…An′内接于边长为1的正n边形A1A2…An，（n≥4），思考会有相应的什么结论？请提出一个的命题，并给与正确解答．
注意：第（3）题中所提问题单独给分，解答也单独给分．本题按照所提问题的难度分层给分，解答也相应给分，如果同时提出两个问题，则就高不就低，解答也相同处理．
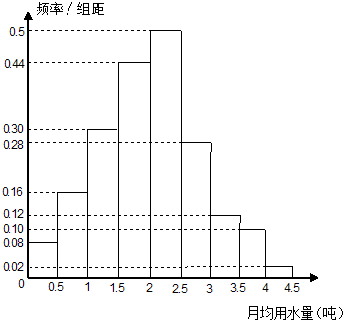我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市政府为了节约生活用水，计划在本市试行居民生活用水定额管理，为此市政府首先采用抽样调查的方法获得了n位居民某年的月均用水量（单位：吨）．根据所得的n个数据按照区间[0，0.5），[0.5，1），[1，1.5），[1.5，2），[2，2.5），[2.5，3），[3，3.5），[3.5，4），[4，4.5]进行分组，得到频率分布直方图如图（1）若已知n位居民中月均用水量小于1吨的人数是12，求n位居民中月均用水量分别在区间[2，2.5）和[2.5，3）内的人数；
（2）在该市居民中随意抽取10位，求至少有2位居民月均用水量在区间[2，2.5）或[2.5，3）内的概率．（精确到0.01．参考数据：0.619≈0.012，0.6110≈0.0071） 查看习题详情和答案>>
某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数图象（部分）刻画了该公司年初以来累积利润s（万元）与销售时间t（月）之间的关系（即前t个月的利润总和s与t之间的关系）．根据图象提供的信息解答下列问题：（1）由已知图象上的三点坐标，求累积利润s（万元）与时间t（月）之间的函数关系式；
（2）求截止到第几月末公司累积利润可达到30万元；
（3）求第八个月该公司所获利润是多少万元？
设函数f（x）=x2+x．（1）解不等式：f（x）＜0；（2）请先阅读下列材料，然后回答问题．
材料：已知函数g（x）=
，问函数g（x）是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，说明理由．一个同学给出了如下解答：
解：令u=-f（x）=-x2-x，则u=-（x+
）2+
，
当x=-
时，u有最大值，umax=
，显然u没有最小值，
∴当x=-
时，g（x）有最小值4，没有最大值．
请回答：上述解答是否正确？若不正确，请给出正确的解答；
（3）设an=
，请提出此问题的一个结论，例如：求通项an．并给出正确解答．
注意：第（3）题中所提问题单独给分，．解答也单独给分．本题按照所提问题的难度分层给分，解答也相应给分，如果同时提出两个问题，则就高不就低，解答也相同处理．
查看习题详情和答案>>
材料：已知函数g（x）=
，问函数g（x）是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，说明理由．一个同学给出了如下解答：解：令u=-f（x）=-x2-x，则u=-（x+
）2+，当x=-
时，u有最大值，umax=，显然u没有最小值，∴当x=-
时，g（x）有最小值4，没有最大值．请回答：上述解答是否正确？若不正确，请给出正确的解答；
（3）设an=
，请提出此问题的一个结论，例如：求通项an．并给出正确解答．注意：第（3）题中所提问题单独给分，．解答也单独给分．本题按照所提问题的难度分层给分，解答也相应给分，如果同时提出两个问题，则就高不就低，解答也相同处理．
查看习题详情和答案>>