摘要：19． 已知数列中.=1, , (1)是否存在常数.使得数列是等比数列.若存在.求的值.若不存在.说明理由. (2)设.数列的前n项和为.是否存在常数c,使得 成立?并证明你的结论. (3)设.,证明<<. 解:(1)设可化为. 即.故.得. 又.所以存在.使得数列是等比数列. 得.得.所以. 要使得成立. 则有.得.所以.存在常数.使得成立. (3)证明:因为.所以.而. 所以. 又当时..符合. 当时.. 得. 综上.<<得证.
网址：http://m.1010jiajiao.com/timu_id_4381851[举报]
(本小题满分14分)
已知数列{an}和{bn}满足：a1=λ，an+1=
其中λ为实数，n为正整数。
（Ⅰ）对任意实数λ，证明数列{an}不是等比数列；
（Ⅱ）试判断数列{bn}是否为等比数列，并证明你的结论；
（Ⅲ）设0＜a＜b，Sn为数列{bn}的前n项和。是否存在实数λ，使得对任意正整数n，都有
a＜Sn＜b?若存在，求λ的取值范围；若不存在，说明理由。
查看习题详情和答案>>(本小题满分14分)
已知数列{an}和{bn}满足：a1=λ，an+1=
其中λ为实数，n为正整数。
（Ⅰ）对任意实数λ，证明数列{an}不是等比数列；
（Ⅱ）试判断数列{bn}是否为等比数列，并证明你的结论；
（Ⅲ）设0＜a＜b，Sn为数列{bn}的前n项和。是否存在实数λ，使得对任意正整数n，都有
a＜Sn＜b?若存在，求λ的取值范围；若不存在，说明理由。
查看习题详情和答案>>(本小题满分14分)
已知数列{an}和{bn}满足：a1=λ，an+1=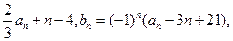
其中λ为实数，n为正整数。
（Ⅰ）对任意实数λ，证明数列{an}不是等比数列；
（Ⅱ）试判断数列{bn}是否为等比数列，并证明你的结论；
（Ⅲ）设0＜a＜b，Sn为数列{bn}的前n项和。是否存在实数λ，使得对任意正整数n，都有
a＜Sn＜b?若存在，求λ的取值范围；若不存在，说明理由。
其中λ为实数，n为正整数。
，其中
是首项为1，公差为1的等差数列；
是公差为
的等差数列；
是公差为
的等差数列（
）.
，求
关于
是公差为
的等差数列，……，依次类推，把已知数列推广为无穷数列. 提出同（2）类似的问题（（2）应当作为特例），并进行研究，你能得到什么样的结论？