摘要：19．设数列{an}的各项为正数.若对任意的正整数n, an与2的等差中项等于其前n项和n与2的等比中项.求{an}的通项公式.
网址：http://m.1010jiajiao.com/timu_id_4381178[举报]
设数列{an}的各项都为正数，其前n项和为Sn，已知对任意n∈N*，Sn是an2和an的等差中项．
（Ⅰ）证明数列{an}为等差数列，并求数列{an}的通项公式；
（Ⅱ）证明
+
+…+
＜2；
（Ⅲ）设集合M={m|m=2k，k∈Z，且1000≤k＜1500}，若存在m∈M，使对满足n＞m的一切正整数n，不等式Sn-1005＞
恒成立，求这样的正整数m共有多少个？
查看习题详情和答案>>
（Ⅰ）证明数列{an}为等差数列，并求数列{an}的通项公式；
（Ⅱ）证明
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
（Ⅲ）设集合M={m|m=2k，k∈Z，且1000≤k＜1500}，若存在m∈M，使对满足n＞m的一切正整数n，不等式Sn-1005＞
| ||
| 2 |
设数列{an}的各项都是正数，记Sn为数列{an}的前n项和，且对任意n∈N*，都有a13+a23+a33+…+an3=Sn2．
（Ⅰ）求证：an2=2Sn-an；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）若bn=3n+(-1)n-1λ•2an（λ为非零常数，n∈N*），问是否存在整数λ，使得对任意 n∈N*，都有bn+1＞bn． 查看习题详情和答案>>
（Ⅰ）求证：an2=2Sn-an；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）若bn=3n+(-1)n-1λ•2an（λ为非零常数，n∈N*），问是否存在整数λ，使得对任意 n∈N*，都有bn+1＞bn． 查看习题详情和答案>>
设数列{an}的各项都是正数，且对任意n∈N*，都有a13+a23+a33+…+=Sn2，其中Sn为数列{an}的前n项和．
（I）求证：an2=2Sn-an；
（II）求数列{an}的通项公式；
（III）若bn=3n+（-1）n-1λ•2an（λ为非零常数，n∈N*），问是否存在整数λ，使得对任意n∈N*，都有bn+1＞bn，若存在，求出λ的值；若不存在，说明理由． 查看习题详情和答案>>
（I）求证：an2=2Sn-an；
（II）求数列{an}的通项公式；
（III）若bn=3n+（-1）n-1λ•2an（λ为非零常数，n∈N*），问是否存在整数λ，使得对任意n∈N*，都有bn+1＞bn，若存在，求出λ的值；若不存在，说明理由． 查看习题详情和答案>>
＋…＋
＝
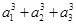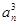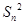，记Sn为数列{an}的前n项和．