摘要:答案:m⊥α.n⊥β.α⊥βm⊥n.或m⊥n.m⊥α. n⊥βα⊥β. 解析:假设①.③.④为条件.即m⊥n.n⊥β.m⊥α成立. 如图1-9.过m上一点P作PB∥n.则PB⊥m.PB⊥β.设垂足为B. 又设m⊥α的垂足为A. 过PA.PB的平面与α.β的交线l交于点C. 因为l⊥PA.l⊥PB.所以l⊥平面PAB.得l⊥AC.l⊥BC.∠ACB是二面角α-l-β的平面角. 显然∠APB+∠ACB=180°.因为PA⊥PB.所以∠ACB=90°.得α⊥β.由①.③.④推得②成立. 反过来.如果②.③.④成立.与上面证法类似可得①成立. 评述:本题主要考查线线.线面.面面之间关系的判定与性质.但题型较新颖.主要表现在:题目以立体几何知识为背景.给出了若干材料.要求学生能将其组装成具有一定逻辑关系的整体.解题的关键是将符号语言转化为图形语言.考查知识立足课本.对空间想象能力.分析问题的能力.操作能力和思维的灵活性等方面要求较高.体现了加强能力考查的方向.
网址:http://m.1010jiajiao.com/timu_id_4380592[举报]
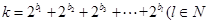 ,且
,且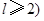 ,求m的最小值.
,求m的最小值.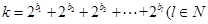 ,且
,且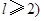 ,求m的最小值.
,求m的最小值.