如图，

填空：

因为∠1＋∠2＝(已知)，所以AB∥CD(　　)，

因为AB∥EF(已知)，所以∠1＋∠3＝(　　)，

因为∠2＝∠3(同角的补角相等)，所以CD∥EF(　　)．

半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，⊙O与l相切于点F，DC在l上．

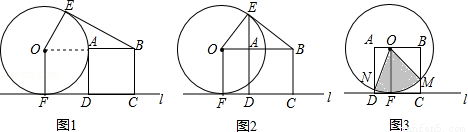
（1）过点B作的一条切线BE，E为切点．

①填空：如图1，当点A在⊙O上时，∠EBA的度数是　    　；

②如图2，当E，A，D三点在同一直线上时，求线段OA的长；

（2）以正方形ABCD的边AD与OF重合的位置为初始位置，向左移动正方形（图3），至边BC与OF重合时结束移动，M，N分别是边BC，AD与⊙O的公共点，求扇形MON的面积的范围．

完成推理填空：如图在△ABC中，已知∠1+∠2=180°，∠3=∠B，试说明∠AED=∠C．
解：∵∠1+∠EFD=180°（邻补角定义），∠1+∠2=180°（已知 ）
∴________　　（ 同角的补角相等 ）
∴________　 （内错角相等，两直线平行）
∴∠ADE=∠3________
∵∠3=∠B________
∴∠ADE=∠B（等量代换）
∴DE∥BC________
∴∠AED=∠C________．