摘要：14．设二次函数f(x)＝ax2+bx+c(a>0).方程f(x)-x＝0的两个根x1.x2满足0<x1<x2<. (1)当x∈(0.x1)时.证明x<f(x)<x1. (2)设函数f(x)的图象关于直线x＝x0对称.证明:x0<. 解:(1)令F(x)＝f(x)-x.因为x1.x2是方程f(x)-x＝0的根.∴F(x)＝a(x-x1)(x-x2).当x∈(0.x1)时 ∵x1<x2得(x-x1)(x-x2)>0又a>0得 F(x)＝a(x-x1)(x-x2)>0即x<f(x) x1-f(x)＝x1-a(x-x1)(x-x2)-x＝(x1-x)[1+a(x-x2)] ∵x1-x>0,1+a(x-x2)＝1+ax-ax2>1-ax2>0 ∴x1-f(x)>0.∴f(x)<x1.∴x<f(x)<x1 (2)依题意知x0＝-.∵x1.x2是方程f(x)-x＝0的根.即x1.x2是方程ax2+(b-1)x+c＝0的根 ∴x1+x2＝-.x0＝-＝＝ ∵ax2<1.∴x0<＝
网址：http://m.1010jiajiao.com/timu_id_4370050[举报]
（12分）（1）设x、y、z
R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
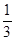（2）设二次函数f (x)＝ax2＋bx＋c （a＞0），方程f (x)－x＝0有两个实根x1，x2，
且满足：0＜x1＜x2＜
，若x(0，x1)。
求证：x＜f (x)＜x1
查看习题详情和答案>>
设二次函数f(x)＝ax2＋bx+c(a＞0），方程f(x)－x＝0的两根x1、x2满足0＜x1＜x2＜
．
． （1）当x∈（0，x1）时，证明x＜f(x)＜x1；
（2）设函数f(x)的图象关于直线x=x0对称；
证明：x0＜
设二次函数f(x)＝x2+ax+a，方程f(x)-x＝0的两根x1和x2满足0<x1<x2<1.
（1）求实数a的取值范围；
（2）试比较f(0)·f(1)-f(0)与的大小，并说明理由
查看习题详情和答案>>
| |||||||||||||||