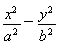摘要：16．已知椭圆C:具有性质:若M.N是椭圆上关于原点对称的两点.点P是椭圆C上任一点.当直线PM.PN的斜率都存在时.记为..那么与之积是与点P位置无关的定值.试对双曲线C:写出具有类似特征的性质并加以证明.
网址：http://m.1010jiajiao.com/timu_id_4368364[举报]
已知椭圆具有性质：若M、N是椭圆C：
+
=1（a＞b＞0）上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM、kPN时，那么kPM与kPN之积是与点P位置无关的定值．试对双曲线C′：
-
=1写出具有类似特性的性质，并加以证明．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，P是椭圆上任意一点，则当直线PM，PN的斜率都存在时，其乘积恒为定值．类比椭圆，写出双曲线C′：
-
=1(a＞0，b＞0)的类似性质，并加以证明．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM、kPN时，那么kPM与kPN之积是与点P位置无关的定值.试对双曲线C′：
写出具有类似特性的性质，并加以证明.
查看习题详情和答案>>
写出具有类似特性的性质，并加以证明.
查看习题详情和答案>>
＝1写出具有类似特性的性质，并加以证明．