摘要: 面积射影定理 . (平面多边形及其射影的面积分别是..它们所在平面所成锐二面角的为).
网址:http://m.1010jiajiao.com/timu_id_4362207[举报]
如图1,在△ABC中AB⊥AC、AD⊥BC,D是垂足,则AB2=BD•BC(射影定理).类似的有命题:在三棱锥A-BCD(图2)中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,则(S△ABC)2=S△BCO•S△BCD(S表示面积.上述命题( )


查看习题详情和答案>>
15、在平面几何里有射影定理:设△ABC的两边AB⊥AC,D是A点在BC边上的射影,则AB2=BD•BC.拓展到空间,在四面体A-BCD中,DA⊥面ABC,点O是A在面BCD内的射影,且O在△BCD内,类比平面三角形射影定理,△ABC,△BOC,△BDC三者面积之间关系为
查看习题详情和答案>>
(S△ABC)2=S△BOC.S△BDC
.14、在平面几何中,有射影定理:“在△ABC中,AB⊥AC,点A在BC边上的射影为D,有AB2=BD•BC.”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥A-BCD中,AD⊥平面ABC,点A在底面BCD上的射影为O,则有

查看习题详情和答案>>
S△ABC2=S△BCO•S△BCD

 中,射影定理可以表示为
中,射影定理可以表示为 ,其中
,其中 分别为角
分别为角 、
、 、
、 的对边,类似以上定理,在四面体
的对边,类似以上定理,在四面体 中,
中, 、
、 、
、 、
、 分别表示△
分别表示△ 、△
、△ 、△
、△ 、△
、△ ,
,  ,
, 分别表示面
分别表示面 中,
中, ,点
,点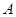 在
在 边上的射影为
边上的射影为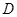 ,有
,有 .”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥
.”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥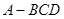 中,
中, 平面
平面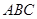 ,点
,点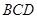 上的射影为
上的射影为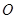 ,则有
.”
,则有
.”