摘要： 已知ΔABC的三个顶点的坐标是A(x1,y1),B(x2,y2),C(x3,y3),求ΔABC的内心I坐标 解:根据角平分线的性质定理结合定比分点的概念解法相当简洁 设∠A的平分线交BC于点D. 则λ= 由两点间的距离公式可求出c=|AB|=, 类似的可求出|CA|, ∴由定比分点的坐标公式可得I(x,y)为:
网址：http://m.1010jiajiao.com/timu_id_4362135[举报]
已知椭圆C：
+
=1的右焦点为F，左顶点为A，点P为曲线D上的动点，以PF为直径的圆恒与y轴相切．
（Ⅰ）求曲线D的方程；
（Ⅱ）设O为坐标原点，是否存在同时满足下列两个条件的△APM？①点M在椭圆C上；②点O为APM的重心．若存在，求出点P的坐标；若不存在，说明理由．（若三角形ABC的三点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则其重心G的坐标为（
，
））
查看习题详情和答案>>
| x2 |
| 4 |
| y2 |
| 3 |
（Ⅰ）求曲线D的方程；
（Ⅱ）设O为坐标原点，是否存在同时满足下列两个条件的△APM？①点M在椭圆C上；②点O为APM的重心．若存在，求出点P的坐标；若不存在，说明理由．（若三角形ABC的三点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则其重心G的坐标为（
| x1+x2+x3 |
| 3 |
| y1+y2+y3 |
| 3 |
已知椭圆C: 
的右焦点为F，左顶点为A，点P为曲线D上的动点，以PF为直径的圆恒与y轴相切. (I)求曲线D的方程；
(II)设O为坐标原点，是否存在同时满足下列两个条件的ΔAPM?
① 点M在椭圆C上;②点O为ΔAPM的重心.
② 若存在，求出点P的坐标；若不存在,说明理由.（若三角形 ABC的三点坐标为
A(x1，y1),B(x2,y2),C(x3，y3)，则其重心G的坐标为(
，
))
（2013•郑州二模）已知椭圆C：
+
=1的右焦点为F，左顶点为A，点P为曲线D上的动点，以PF为直径的圆恒与y轴相切．
（Ⅰ）求曲线D的方程；
（Ⅱ）设O为坐标原点，是否存在同时满足下列两个条件的△APM？①点M在椭圆C上；②点O为APM的重心．若存在，求出点P的坐标；若不存在，说明理由．（若三角形ABC的三点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则其重心G的坐标为（
，
））
查看习题详情和答案>>
| x2 |
| 4 |
| y2 |
| 3 |
（Ⅰ）求曲线D的方程；
（Ⅱ）设O为坐标原点，是否存在同时满足下列两个条件的△APM？①点M在椭圆C上；②点O为APM的重心．若存在，求出点P的坐标；若不存在，说明理由．（若三角形ABC的三点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则其重心G的坐标为（
| x1+x2+x3 |
| 3 |
| y1+y2+y3 |
| 3 |
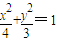的右焦点为F，左顶点为A，点P为曲线D上的动点，以PF为直径的圆恒与y轴相切．
，
））
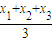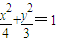的右焦点为F，左顶点为A，点P为曲线D上的动点，以PF为直径的圆恒与y轴相切．
，
））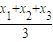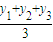