摘要：(二)用0.2000 mol·L-1Na2CO3溶液标定未知浓度的盐酸 (1)把0.2000 mol·L-1Na2CO3溶液装入 滴定管中.从此滴定管中放出20.00mL0.2000 mol·L-1Na2CO3溶液入锥形瓶中,滴2至3滴甲基橙作指示剂.用未知浓度的盐酸来滴定0.2000 mol·L-1Na2CO3溶液.根据 判断滴定终点达到. (2)终点达到时.用去盐酸16.00mL.则盐酸c(HCl)=
网址：http://m.1010jiajiao.com/timu_id_4359302[举报]
（二）选做题
A 在极坐标系中，o是极点，设点A(4，
)，B(4，
)，则点O到直线AB的距离是 ；
B 用0.618法对某一试验进行优选，因素范围是[2000，8000]，则第二个试点x2是 ．
查看习题详情和答案>>
A 在极坐标系中，o是极点，设点A(4，
| π |
| 6 |
| 2π |
| 3 |
B 用0.618法对某一试验进行优选，因素范围是[2000，8000]，则第二个试点x2是
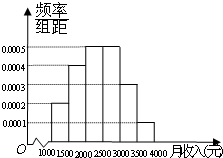（2012•梅州二模）一个社会调查机构就某社区居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图（如图）．（1）为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，求月收入在[1500，2000）（元）段应抽出的人数；
（2）为了估计该社区3个居民中恰有2个月收入在[2000，3000）（元）的概率，采用随机模拟的方法：先由计算器算出0到9之间取整数值的随机数，我们用0，1，2，3，…表示收入在[2000，3000）（元）的居民，剩余的数字表示月收入不在[2000，3000）（元）的居民；再以每三个随机数为一组，代表统计的结果，经随机模拟产生了20组随机数如下：
907 966 191 925 271 932 812 458
569 683 431 257 393 027 556 488
730 113 537 989
据此估计，计算该社区3个居民中恰好有2个月收入在[2000，3000）（元）的概率．
（3）任意抽取该社区6个居民，用ξ表示月收入在（2000，3000）（元）的人数，求ξ的数学期望．
（2012•梅州二模）一个社会调查机构就某社区居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）．（1）为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，求月收入在[1500，2000）（元）段应抽出的人数；
（2）估计该社区居民月收人的平均数；
（3）为了估计该社区3个居民中恰有2个月收入在[2000，3000）（元）的概率，采用随机模拟的方法：先由计算器算出0到9之间取整数值的随机数，我们用0，1，2，3，…表示收入在[2000，3000）（元）的居民，剩余的数字表示月收入不在[2000，3000）（元）的居民；再以每三个随机数为一组，代表统计的结果，经随机模拟产生了20组随机数如下：
907 966 191 925 271 932 812 458
569 683 431 257 393 027 556 488
730 113 537 989
据此估计，计算该社区3个居民中恰好有2个月收入在[2000，3000）（元）的概率．
，则点O到直线AB的距离是 ；
，则点O到直线AB的距离是________；