摘要:函数f的图象如下图所示.则函数g(x)=f(logax) 的单调减区间是 . 答案 [,1]
网址:http://m.1010jiajiao.com/timu_id_4357699[举报]
如下图所示,图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象。
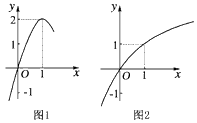
(1)分别求出函数f(x)和g(x)的解析式;
(2)如果函数y=g(f(x))在区间[1,m)上单调递减,求m的取值范围。
查看习题详情和答案>>
(2)如果函数y=g(f(x))在区间[1,m)上单调递减,求m的取值范围。
如下图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
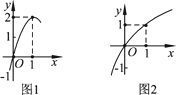
(1)分别求出函数f(x)和g(x)的解析式;
(2)如果函数y=g(f(x))在区间[1,m)上单调递减,求m的取值范围.
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
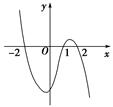

| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(-2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(-2) |
| D.函数f(x)有极大值f(-2)和极小值f(2) |
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )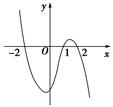
| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(-2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(-2) |
| D.函数f(x)有极大值f(-2)和极小值f(2) |
