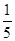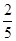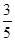摘要: 反函数: (1)存在反函数的条件是对于原来函数值域中的任一个值.都有唯一的值与之对应.故单调函数一定存在反函数.但反之不成立,偶函数只有有反函数,周期函数一定不存在反函数.如函数在区间[1, 2]上存在反函数的充要条件是A. B. C. D. (2)求反函数的步骤:①反求,②互换 .,③注明反函数的定义域.注意函数的反函数不是.而是.如设.求的反函数(答:). (3)反函数的性质: ①反函数的定义域是原来函数的值域.反函数的值域是原来函数的定义域.如单调递增函数满足条件= x .其中≠ 0 .若的反函数的定义域为 .则的定义域是 . ②函数的图象与其反函数的图象关于直线对称.注意函数的图象与的图象相同.如(1)已知函数的图象过点(1,1),那么的反函数的图象一定经过点 已知函数.若函数与的图象关于直线对称.求的值(答:), ③.如(1)已知函数.则方程的解 设函数f(x)的图象关于点(1,2)对称.且存在反函数.f (4)=0.则= ④互为反函数的两个函数具有相同的单调性和奇函数性.如已知是上的增函数.点在它的图象上.是它的反函数.那么不等式的解集为 , ⑤设的定义域为A.值域为B.则有. .但.
网址:http://m.1010jiajiao.com/timu_id_4357256[举报]
对于函数y=f(x),有下列五个命题:
①若y=f(x)存在反函数,且与反函数图象有公共点,则公共点一定在直线y=x上;
②若y=f(x)在R上有定义,则y=f(|x|)一定是偶函数;
③若y=f(x)是偶函数,且f(x)=0有解,则解的个数一定是偶数;
④若T(T≠0)是函数y=f(x)的周期,则nT(n∈N),也是函数y=f(x)的周期;
⑤f(0)=0是函数y=f(x)为奇函数的充分也不必要条件.
从中任意抽取一个,恰好是真命题的概率为( )
①若y=f(x)存在反函数,且与反函数图象有公共点,则公共点一定在直线y=x上;
②若y=f(x)在R上有定义,则y=f(|x|)一定是偶函数;
③若y=f(x)是偶函数,且f(x)=0有解,则解的个数一定是偶数;
④若T(T≠0)是函数y=f(x)的周期,则nT(n∈N),也是函数y=f(x)的周期;
⑤f(0)=0是函数y=f(x)为奇函数的充分也不必要条件.
从中任意抽取一个,恰好是真命题的概率为( )
对于函数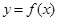 ,有下列五个命题:
,有下列五个命题:
①若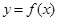 存在反函数,且与反函数图象有公共点,则公共点一定在直线
存在反函数,且与反函数图象有公共点,则公共点一定在直线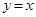 上;
上;
②若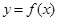 在
在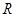 上有定义,则
上有定义,则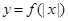 一定是偶函数;
一定是偶函数;
③若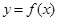 是偶函数,且
是偶函数,且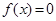 有解,则解的个数一定是偶数;
有解,则解的个数一定是偶数;
④若 是函数
是函数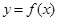 的周期,则
的周期,则 ,也是函数
,也是函数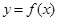 的周期;
的周期;
⑤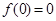 是函数
是函数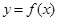 为奇函数的充分不必要条件。
为奇函数的充分不必要条件。
从中任意抽取一个,恰好是真命题的概率为 ( )
A.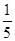 B.
B.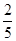 C.
C.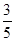 D.
D.
查看习题详情和答案>>
对于函数y=f(x),有下列五个命题:
①若y=f(x)存在反函数,且与反函数图象有公共点,则公共点一定在直线y=x上;
②若y=f(x)在R上有定义,则y=f(|x|)一定是偶函数;
③若y=f(x)是偶函数,且f(x)=0有解,则解的个数一定是偶数;
④若T(T≠0)是函数y=f(x)的周期,则nT(n∈N),也是函数y=f(x)的周期;
⑤f(0)=0是函数y=f(x)为奇函数的充分也不必要条件.
从中任意抽取一个,恰好是真命题的概率为( )
查看习题详情和答案>>
①若y=f(x)存在反函数,且与反函数图象有公共点,则公共点一定在直线y=x上;
②若y=f(x)在R上有定义,则y=f(|x|)一定是偶函数;
③若y=f(x)是偶函数,且f(x)=0有解,则解的个数一定是偶数;
④若T(T≠0)是函数y=f(x)的周期,则nT(n∈N),也是函数y=f(x)的周期;
⑤f(0)=0是函数y=f(x)为奇函数的充分也不必要条件.
从中任意抽取一个,恰好是真命题的概率为( )
A.
| B.
| C.
| D.
|
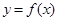 ,有下列五个命题:
,有下列五个命题: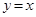 上;
上;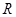 上有定义,则
上有定义,则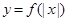 一定是偶函数;
一定是偶函数;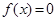 有解,则解的个数一定是偶数;
有解,则解的个数一定是偶数;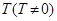 是函数
是函数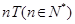 ,也是函数
,也是函数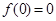 是函数
是函数