摘要: 如何解抽象函数问题?
网址:http://m.1010jiajiao.com/timu_id_4356784[举报]
阅读下列材料,然后解答问题;对于任意实数x,符号[x]表示“不超过x的最大整
数”,在数轴上,当x是整数,[x]是x,当x不是整数时,[x]是x左侧的第一个整数,这个函数叫做“取整函数”,也叫高斯(Gauss)函数,如[-2]=-2、[-1.5]=-2、[2.5]=2 定义函数{x}=x-[x],给出下列四个命题;
①函数[x]的定义域是R,值域为[0,1];
②方程{x}=
有无数个解;
③函数{x}是周期函数;
④函数{x}是增函数.
其中正确命题的序号是 (写出所有正确结论的序号)
查看习题详情和答案>>
数”,在数轴上,当x是整数,[x]是x,当x不是整数时,[x]是x左侧的第一个整数,这个函数叫做“取整函数”,也叫高斯(Gauss)函数,如[-2]=-2、[-1.5]=-2、[2.5]=2 定义函数{x}=x-[x],给出下列四个命题;
①函数[x]的定义域是R,值域为[0,1];
②方程{x}=
| 1 | 2 |
③函数{x}是周期函数;
④函数{x}是增函数.
其中正确命题的序号是
解::因为![]() ,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=
,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=![]() 与y=-
与y=-![]() 在(0,+
在(0,+![]() )上都是增函数,因此
)上都是增函数,因此![]() 在(0,+
在(0,+![]() )上是增函数,所以零点个数只有一个方法2:把函数
)上是增函数,所以零点个数只有一个方法2:把函数![]() 的零点个数个数问题转化为判断方程
的零点个数个数问题转化为判断方程![]() 解的个数问题,近而转化成判断
解的个数问题,近而转化成判断![]() 与
与![]() 交点个数问题,在坐标系中画出图形
交点个数问题,在坐标系中画出图形
由图看出显然一个交点,因此函数![]() 的零点个数只有一个
的零点个数只有一个
袋中有50个大小相同的号牌,其中标着0号的有5个,标着n号的有n个(n=1,2,…9),现从袋中任取一球,求所取号码的分布列,以及取得号码为偶数的概率.
查看习题详情和答案>> 就可以得出问题的结论.
就可以得出问题的结论. ,符号[
,符号[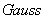 )函数,如[-2]=-2、[-1.5]=-2、[2.5]=2 定义函数{
)函数,如[-2]=-2、[-1.5]=-2、[2.5]=2 定义函数{ ,值域为[0,1]
,值域为[0,1] 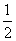 有无数个解;
有无数个解;