摘要: 你熟悉周期函数的定义吗? 函数.T是一个周期.) 如:
网址:http://m.1010jiajiao.com/timu_id_4356780[举报]
(2008•上海一模)观察数列:
①1,-1,1,-1,…;
②正整数依次被4除所得余数构成的数列1,2,3,0,1,2,3,0,…;
③an=tan
,n=1,2,3,…
(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列{an},如果
(2)若数列{an}满足an+2=an+1-an,n∈N*,Sn为{an}的前n项和,且S2=2008,S3=2010,证明{an}为周期数列,并求S2008;
(3)若数列{an}的首项a1=p,p∈[0,
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
查看习题详情和答案>>
①1,-1,1,-1,…;
②正整数依次被4除所得余数构成的数列1,2,3,0,1,2,3,0,…;
③an=tan
| nπ |
| 3 |
(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列{an},如果
存在正整数T
存在正整数T
,对于一切正整数n都满足an+T=an
an+T=an
成立,则称数列{an}是以T为周期的周期数列;(2)若数列{an}满足an+2=an+1-an,n∈N*,Sn为{an}的前n项和,且S2=2008,S3=2010,证明{an}为周期数列,并求S2008;
(3)若数列{an}的首项a1=p,p∈[0,
| 1 |
| 2 |
观察数列:
①![]() ;②正整数依次被4除所得余数构成的数列
;②正整数依次被4除所得余数构成的数列![]() ;
;
③![]()
(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列![]() ,如果________________________,对于一切正整数
,如果________________________,对于一切正整数![]() 都满足___________________________成立,则称数列
都满足___________________________成立,则称数列![]() 是以
是以![]() 为周期的周期数列;
为周期的周期数列;
(2)若数列![]() 满足
满足![]() 为
为![]() 的前
的前![]() 项和,且
项和,且![]() ,证明
,证明![]() 为周期数列,并求
为周期数列,并求![]() ;
;
(3)若数列![]() 的首项
的首项![]() ,且
,且![]() ,判断数列
,判断数列![]() 是否为周期数列,不用证明.
是否为周期数列,不用证明.
观察数列:
①1,-1,1,-1,…;
②正整数依次被4除所得余数构成的数列1,2,3,0,1,2,3,0,…;
③an=tan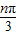 ,n=1,2,3,…
,n=1,2,3,…
(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列{an},如果______,对于一切正整数n都满足______成立,则称数列{an}是以T为周期的周期数列;
(2)若数列{an}满足an+2=an+1-an,n∈N*,Sn为{an}的前n项和,且S2=2008,S3=2010,证明{an}为周期数列,并求S2008;
(3)若数列{an}的首项a1=p,p∈[0, ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
查看习题详情和答案>>
①1,-1,1,-1,…;
②正整数依次被4除所得余数构成的数列1,2,3,0,1,2,3,0,…;
③an=tan
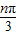 ,n=1,2,3,…
,n=1,2,3,…(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列{an},如果______,对于一切正整数n都满足______成立,则称数列{an}是以T为周期的周期数列;
(2)若数列{an}满足an+2=an+1-an,n∈N*,Sn为{an}的前n项和,且S2=2008,S3=2010,证明{an}为周期数列,并求S2008;
(3)若数列{an}的首项a1=p,p∈[0,
 ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.查看习题详情和答案>>
观察数列:
①1,-1,1,-1,…;
②正整数依次被4除所得余数构成的数列1,2,3,0,1,2,3,0,…;
③an=tan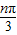 ,n=1,2,3,…
,n=1,2,3,…
(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列{an},如果______,对于一切正整数n都满足______成立,则称数列{an}是以T为周期的周期数列;
(2)若数列{an}满足an+2=an+1-an,n∈N*,Sn为{an}的前n项和,且S2=2008,S3=2010,证明{an}为周期数列,并求S2008;
(3)若数列{an}的首项a1=p,p∈[0, ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
查看习题详情和答案>>
①1,-1,1,-1,…;
②正整数依次被4除所得余数构成的数列1,2,3,0,1,2,3,0,…;
③an=tan
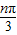 ,n=1,2,3,…
,n=1,2,3,…(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列{an},如果______,对于一切正整数n都满足______成立,则称数列{an}是以T为周期的周期数列;
(2)若数列{an}满足an+2=an+1-an,n∈N*,Sn为{an}的前n项和,且S2=2008,S3=2010,证明{an}为周期数列,并求S2008;
(3)若数列{an}的首项a1=p,p∈[0,
 ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.查看习题详情和答案>>
观察数列:
①1,-1,1,-1,…;
②正整数依次被4除所得余数构成的数列1,2,3,0,1,2,3,0,…;
③an=tan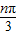 ,n=1,2,3,…
,n=1,2,3,…
(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列{an},如果______,对于一切正整数n都满足______成立,则称数列{an}是以T为周期的周期数列;
(2)若数列{an}满足an+2=an+1-an,n∈N*,Sn为{an}的前n项和,且S2=2008,S3=2010,证明{an}为周期数列,并求S2008;
(3)若数列{an}的首项a1=p,p∈[0, ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
查看习题详情和答案>>
①1,-1,1,-1,…;
②正整数依次被4除所得余数构成的数列1,2,3,0,1,2,3,0,…;
③an=tan
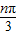 ,n=1,2,3,…
,n=1,2,3,…(1)对以上这些数列所共有的周期特征,请你类比周期函数的定义,为这类数列下一个周期数列的定义:对于数列{an},如果______,对于一切正整数n都满足______成立,则称数列{an}是以T为周期的周期数列;
(2)若数列{an}满足an+2=an+1-an,n∈N*,Sn为{an}的前n项和,且S2=2008,S3=2010,证明{an}为周期数列,并求S2008;
(3)若数列{an}的首项a1=p,p∈[0,
 ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.查看习题详情和答案>>