摘要:过椭圆左焦点的焦点弦为AB.则.过右焦点的弦, [典型例题] 例1. 已知椭圆 及直线 . (1)当 为何值时.直线与椭圆有公共点? (2)若直线被椭圆截得的弦长为 .求直线的方程. 分析:直线与椭圆有公共点.等价于它们的方程组成的方程组有解. 因此.只须考虑方程组消元后所得的一元二次方程的根的判别式. 已知弦长.由弦长公式就可求出 . 解:(1)把直线方程 代入椭圆方程 得 .即 . . 解得 . (2)设直线与椭圆的两个交点的横坐标为 . . 由(1)得. . 根据弦长公式得 . 解得 . 因此.所求直线的方程为 . 说明:处理有关直线与椭圆的位置关系问题及有关弦长问题.采用的方法与处理直线和圆的有所区别. 这里解决直线与椭圆的交点问题.一般考虑判别式 ,解决弦长问题.一般应用弦长公式. 用弦长公式.若能合理运用韦达定理.可大大简化运算过程. 例2. 直线 与双曲线 相交于 . 两点. 当 为何值时.以 为直径的圆经过坐标原点. 解:由方程组: 得 因为直线与双曲线交于 . 两点 ∴ 解得 . 设 . .则: . . 而以 为直径的圆过原点.则 . ∴ . . 于是 . 即 . 解得 满足条件. 故当 时.以 为直径的圆过原点. 例3. 斜率为1的直线经过抛物线 的焦点.与抛物线相交于两点 . .求线段 的长. 解:由抛物线的标准方程可知.焦点 .准线方程 . 由题设.直线 的方程为: . 代入抛物线方程 .整理得: . 解法一:解上述方程得: . 分别代入直线方程得: 即 坐标分别为 . . 解法二:设 . .则: =8 解法三:设 . B(x2.y2). 由抛物线定义可知. 等于点 到准线 的距离 . 即 同理 点拨:(1)解法一利用传统的基本方法求出 两点坐标.再利用两点间距离公式求出 的长.解法二没有利用直线求出 坐标.而是利用韦达定理找到 与 的关系.利用直线截二次曲线的弦长公式 求得.这是典型的设而不求思想方法比解法一先进.解法三充分利用抛物线的定义.把过焦点的这一特殊的弦分成两个半径的和.转化为准线的距离.这是思维质的飞跃. (2)抛物线 上一点 到焦点 的距离 这就是抛物线的焦半径公式.焦点弦长 例4. 若直线 与抛物线 交于A.B两点.且AB中点的横坐标为2.求此直线方程. 分析:由直线与抛物线相交利用韦达定理列出k的方程求解. 另由于已知与直线斜率及弦中点坐标有关.故也可利用“作差法 求k. 解法一:设 . .则由: 可得: ∵直线与抛物线相交. 且 .则 ∵AB中点横坐标为: 解得: 或 故所求直线方程为: 解法二:设 . .则有 两式作差解: . 即 故 或 则所求直线方程为: 例5. (1)设抛物线 被直线 截得的弦长为 .求k值. 中的弦为底边.以x轴上的点P为顶点作三角形.当三角形的面积为9时.求P点坐标. 分析:(1)题可利用弦长公式求k.(2)题可利用面积求高.再用点到直线距离求P点坐标. 解:(1)由 得: 设直线与抛物线交于 与 两点. 则有: .即 (2) .底边长为 . ∴三角形高 ∵点P在x轴上.∴设P点坐标是 则点P到直线 的距离就等于h.即 或 . 即所求P点坐标是. [模拟试题]
网址:http://m.1010jiajiao.com/timu_id_4355962[举报]
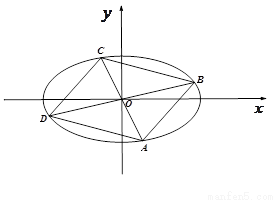
如图椭圆![]() (a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.
(a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.
(1)求椭圆的离心率;
(2)若平行四边形OCED的面积为![]() , 求椭圆方程.
, 求椭圆方程.

(08年宝山区模拟理 ) (18分)已知椭圆C:![]() (a>b>0)的一个焦点到长轴的两个端点的距离分别为
(a>b>0)的一个焦点到长轴的两个端点的距离分别为![]() 。
。
(1)求椭圆的方程;
(2)设过定点M(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
(3)如图,过原点O任意作两条互相垂直的直线与椭圆![]() (a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件。
(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件。

已知椭圆
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
(1)求 的标准方程;(2)四边形ABCD的顶点在椭圆
的标准方程;(2)四边形ABCD的顶点在椭圆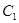 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求四边形ABCD的面积;
查看习题详情和答案>>
 (a>b>0)的右焦点交椭圆于A.B两点,P为直线
(a>b>0)的右焦点交椭圆于A.B两点,P为直线 上任意一点,则∠APB为 (
)
上任意一点,则∠APB为 (
) (a>b>0)的右焦点交椭圆于A.B两
(a>b>0)的右焦点交椭圆于A.B两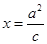 上任意一点,则∠APB为 ( )
上任意一点,则∠APB为 ( )



