摘要:12.在平面四边形ABCD中.已知AB=BC=CD=a...沿AC将四边形折成直二面角B-AC-D. (1)求证:面ABC⊥面BCD, (2)求面ABD与面ACD所成的角. 解:(1)∵AB=BC...即AC⊥CD. 又面ABC⊥面ACD.交线为AC.∴CD⊥面ABC.∴面ABC⊥面BCD. (2)过B作BE⊥AC于E.过E作EF⊥AD于F. ∵面ABC⊥面ACD.AC为交线. 又∵BE⊥AC.∴BE⊥面ACD.∴EF为BF在平面ACD内的射影. 又∵EF⊥AD.∴AD⊥BF.∴∠BFE为二面角B-AD-C的平面角. ∵AB=BC.BE⊥AC.∴E是AC的中点.∴. 又. ∴. .即为所求. 考查异面直线所成的角.直线与平面所成的角.平面与平面所成的二面角.要求掌握斜线在平面上的射影.直线与平面所成的角.二面角.二面角的平面角 理清求空间的角方法:一般是化归为求两条相交直线的夹角.通常应用“线线角抓平移.线面角抓射影.面面角抓平面角 而达到化归目的.注意空间的角的计算应由“作.证.算 三个部分组成.首先应作出必要的辅助平面或辅助线,然后通过推理.论证找到某角就是所求的角,最后才是计算. 对于折叠问题, 要注意线的长度.角的大小及线线关系的变与不变.
网址:http://m.1010jiajiao.com/timu_id_4353128[举报]
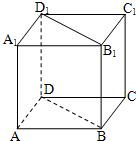 已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是( )
已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是( )| A、两两异面 | B、两两平行 | C、交于一点 | D、两两相交 |
已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是( )
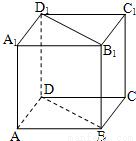
A.两两异面
B.两两平行
C.交于一点
D.两两相交
查看习题详情和答案>>

A.两两异面
B.两两平行
C.交于一点
D.两两相交
查看习题详情和答案>>
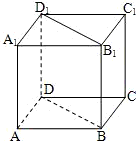 已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是
已知在空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且BG:GC=DH:HC=2:1,则EG、FH、AC的位置关系是
- A.两两异面
- B.两两平行
- C.交于一点
- D.两两相交
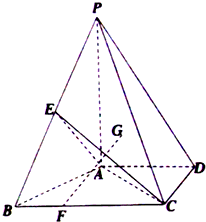 已知四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=2,G为△PAC的重心,E为PB的中点,F在BC上,且CF=2FB.
已知四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=2,G为△PAC的重心,E为PB的中点,F在BC上,且CF=2FB.