摘要：4．给出下列命题 ①空间四点共面.则其中必有三点共线, ②空间四点不共面.则其中任何三点不共线, ③空间四点中有三点共线.则此四点共面, ④空间四点中任何三点不共线.则此四点不共面． 其中正确的命题是 A．②③ B．①②③ C．①③ D．②③④ 考查平面基本性质．要求能够根据图形想象空间两条直线.直线与平面的位置关系,能够正确文字语言.符号语言.图形语言之间的转化．能正确运用平面基本性质证明有关三线共点.三点共线或点.线共面等问题．
网址：http://m.1010jiajiao.com/timu_id_4353093[举报]
给出下列命题：
①“sinα＞sinβ”是“α＞β”的既不充分又不必要条件；
②若f（x）在某区间M上为增函数，则对于该区间上的任意x，总有f′（x）＞0；
③设空间任意一点O和不共线三点A、B、C，若点P满足向量关系
=x
+y
+z
，则P、A、B、C四点共面；
④若取值为x1，x2，x3…xn的频率分别为p1，p2，p3…pn，则其平均数为
xipi．
其中所有真命题的序号是
查看习题详情和答案>>
①“sinα＞sinβ”是“α＞β”的既不充分又不必要条件；
②若f（x）在某区间M上为增函数，则对于该区间上的任意x，总有f′（x）＞0；
③设空间任意一点O和不共线三点A、B、C，若点P满足向量关系
| OP |
| OA |
| OB |
| OC |
④若取值为x1，x2，x3…xn的频率分别为p1，p2，p3…pn，则其平均数为
| n |
 |
| i=1 |
其中所有真命题的序号是
①④
①④
．给出下列命题：
①“sinα＞sinβ”是“α＞β”的既不充分又不必要条件；
②若f（x）在某区间M上为增函数，则对于该区间上的任意x，总有f′（x）＞0；
③设空间任意一点O和不共线三点A、B、C，若点P满足向量关系
=x
+y
+z
，则P、A、B、C四点共面；
④若取值为x1，x2，x3…xn的频率分别为p1，p2，p3…pn，则其平均数为
xipi．
其中所有真命题的序号是______．
查看习题详情和答案>>
①“sinα＞sinβ”是“α＞β”的既不充分又不必要条件；
②若f（x）在某区间M上为增函数，则对于该区间上的任意x，总有f′（x）＞0；
③设空间任意一点O和不共线三点A、B、C，若点P满足向量关系
| OP |
| OA |
| OB |
| OC |
④若取值为x1，x2，x3…xn的频率分别为p1，p2，p3…pn，则其平均数为
| n |
 |
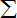| i=1 |
其中所有真命题的序号是______．
给出下列四个命题：①在空间，若四点不共面，则每三个点一定不共线；②已知命题p、q，“非p为假命题”是“p或q是真命题”的必要不充分条件；③函数y=x+
的最小值为2；④若奇函数f（x）对于定义域内任意x都有f（x）=f（1-x），则f（x）为周期函数．其中错误 命题的序号为 ．
查看习题详情和答案>>
| 1 | x |
的最小值为2；④若奇函数f（x）对于定义域内任意x都有f（x）=f（1-x），则f（x）为周期函数．其中错误 命题的序号为 ．