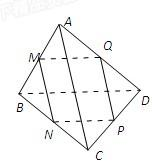
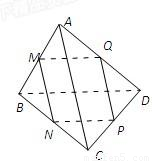
摘要:例1.如图.已知M.N.P.Q分别是空间四边形ABCD的边AB.BC.CD.DA的中点. 求证:(1)线段MP和NQ相交且互相平分,(2)AC∥平面MNP.BD∥平面MNP. 证明:(1) ∵M.N是AB.BC的中点.∴MN∥AC.MN=AC. ∵P.Q是CD.DA的中点.∴PQ∥CA.PQ=CA. ∴MN∥QP.MN=QP.MNPQ是平行四边形. ∴□MNPQ的对角线MP.NQ相交且互相平分. .AC∥MN.记平面MNP(即平面MNPQ)为α.显然ACËα. 否则.若ACÌα. 由A∈α.M∈α.得B∈α, 由A∈α.Q∈α.得D∈α.则A.B.C.D∈α. 与已知四边形ABCD是空间四边形矛盾. 又∵MNÌα.∴AC∥α. 又AC Ëα.∴AC∥α.即AC∥平面MNP. 同理可证BD∥平面MNP. 例2.四面体中.分别为的中点.且. .求证:平面 证明:取的中点.连结.∵分别为的中点.∴ .又∴.∴在中. ∴.∴.又.即. ∴平面 例3. 如图.直三棱柱中..侧棱.侧面的两条对角线交于点.的中点为.求证:平面 证明:连结.∵∴.在直三棱柱中 .∴平面.∵. ∴.∴.∵是侧面的两条对角 线的交点.∴是与的中点.∴.连结 .取的中点.连结.则. ∵平面.∴平面.∴是在 平面内的射影.在中. 在中..∴ ∴.∴.∴平面 例4.如图.矩形所在的平面.分别是的中点. (1)求证:平面, (2)求证: (3)若.求证:平面
网址:http://m.1010jiajiao.com/timu_id_4351985[举报]
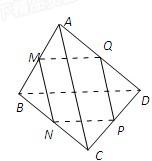 如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.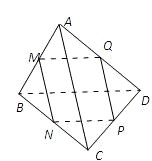 如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.