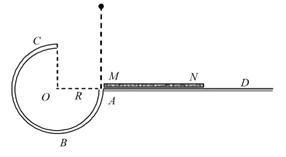
摘要:如图2所示.一小球从光滑圆弧轨道顶端由静止开始下滑.进入光 滑水平面又压缩弹簧.在此过程中.小球重力势能和动能的最大值分 别为Ep和Ek.弹簧弹性势能的最大值为Ep′.则它们之间的关系为( ) 图2 A.Ep=Ek=Ep′ B.Ep>Ek>Ep′ C.Ep=Ek+Ep′ D.Ep+Ek=Ep′ 解析:当小球处于最高点时.重力势能最大,当小球刚滚到水平面时重力势能全部转化为动能.此时动能最大,当小球压缩弹簧到最短时动能全部转化为弹性势能.弹性势能最大.由机械能守恒定律可知Ep=Ek=Ep′.故答案选A. 答案:A
网址:http://m.1010jiajiao.com/timu_id_4346255[举报]
如图2所示,一小球从光滑圆弧轨道顶端由静止开始下滑,进入光
滑水平面又压缩弹簧.在此过程中,小球重力势能和动能的最大值分
别为Ep和Ek,弹簧弹性势能的最大值为Ep′,则它们之间的关系为( )
滑水平面又压缩弹簧.在此过程中,小球重力势能和动能的最大值分
别为Ep和Ek,弹簧弹性势能的最大值为Ep′,则它们之间的关系为( )

| A.Ep=Ek=Ep′ | B.Ep>Ek>Ep′ |
| C.Ep=Ek+Ep′ | D.Ep+Ek=Ep′ |
如图2所示,一小球从光滑圆弧轨道顶端由静止开始下滑,进入光
滑水平面又压缩弹簧.在此过程中,小球重力势能和动能的最大值分
别为Ep和Ek,弹簧弹性势能的最大值为Ep′,则它们之间的关系为( ) 
| A.Ep=Ek=Ep′ | B.Ep>Ek>Ep′ |
| C.Ep=Ek+Ep′ | D.Ep+Ek=Ep′ |
如图所示,一小球从光滑圆弧轨道顶端由静止开始下滑,进入光
滑水平面又压缩弹簧.在此过程中,小球重力势能和动能的最大值分
别为Ep和Ek,弹簧弹性势能的最大值为Ep′,则它们之间的关系为( ) 图2
A.Ep=Ek=Ep′ B.Ep>Ek>Ep′
C.Ep=Ek+Ep′ D.Ep+Ek=Ep′
查看习题详情和答案>>
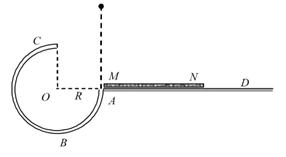
 圆弧形光滑细圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN是放在水平地面上长为3R、厚度不计的垫子,左端M正好位于A点.将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放,不考虑空气阻力.
圆弧形光滑细圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN是放在水平地面上长为3R、厚度不计的垫子,左端M正好位于A点.将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放,不考虑空气阻力.