摘要：解:(1)当a=1时..其定义域是. ---------------------------------1分 令.即.解得或． ∵x>0.舍去． 当时.,当时.． ∴函数在区间(0.1)上单调递增.在区间上单调递减 ----------4分 ∴当x=1时.函数取得最大值.其值为． 当时..即． ∴函数只有一个零点． ---------------------6分 (2)因为其定义域为. 所以-----------------------7分 ①当a=0时.在区间上为增函数.不合题意----------8分 ②当a>0时.等价于.即． 此时的单调递减区间为． 依题意.得解之得 ---------------------------------10分 ③当a<0时.等价于.即· 此时的单调递减区间为. 得 综上.实数a的取值范围是 ---------------------------------12分
网址：http://m.1010jiajiao.com/timu_id_4344409[举报]
设函数y=f（x）是定义域为R 的奇函数，且满足f(x-2)=-f(x)对一切x∈R恒成立，当
-1≤x≤1时，f(x)=x3。则下列四个命题：①f(x)是以4为周期的周期函数；②f(x)在[1，3]上的解析式为f(x)=(2-x)3；③f(x)在
处的切线方程为3x+4y-5=0；④f(x)的图像的对称轴中有x=±1.其中正确的命题是 （ ）
A．① ② ③ B．② ③ ④ C．① ③ ④ D．① ② ③ ④
查看习题详情和答案>>已知函数f（x）=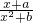
是定义在R上的奇函数，其值域为[-
]．
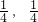（1）试求a、b的值；
（2）函数y=g（x）（x∈R）满足：①当x∈[0，3）时，g（x）=f（x）；②g（x+3）=g（x）lnm（m≠1）．
①求函数g（x）在x∈[3，9）上的解析式；
②若函数g（x）在x∈[0，+∞）上的值域是闭区间，试探求m的取值范围，并说明理由．
查看习题详情和答案>>
已知函数f（x）=
是定义在R上的奇函数，其值域为[-
]．
（1）试求a、b的值；
（2）函数y=g（x）（x∈R）满足：①当x∈[0，3）时，g（x）=f（x）；②g（x+3）=g（x）lnm（m≠1）．
①求函数g（x）在x∈[3，9）上的解析式；
②若函数g（x）在x∈[0，+∞）上的值域是闭区间，试探求m的取值范围，并说明理由．
查看习题详情和答案>>
是定义在R上的奇函数，其值域为[-]．（1）试求a、b的值；
（2）函数y=g（x）（x∈R）满足：①当x∈[0，3）时，g（x）=f（x）；②g（x+3）=g（x）lnm（m≠1）．
①求函数g（x）在x∈[3，9）上的解析式；
②若函数g（x）在x∈[0，+∞）上的值域是闭区间，试探求m的取值范围，并说明理由．
查看习题详情和答案>>