摘要： 解:( 1)由已知得:解得 c=3,b=2 ∴抛物线的线的解析式为 (2)由顶点坐标公式得顶点坐标为(1.4) 所以对称轴为x=1,A,E关于x=1对称.所以E(3,0) 设对称轴与x轴的交点为F 所以四边形ABDE的面积= = = =9 (3)相似 如图.BD= BE= DE= 所以, 即: ,所以是直角三角形 所以,且, 所以.
网址：http://m.1010jiajiao.com/timu_id_4332094[举报]
已知：抛物线y=-x2+（m+2）x+m-1与x轴交于A、B两点（点A、B分别在原点O的左、右两侧），以OA、OB为直径作⊙O1和⊙O2．
（1）请问：⊙O1和⊙O2，能否为等圆？若能，求出其半径的长度；若不能，说明理由；
（2）设抛物线向上平移4个单位后，⊙O1、⊙O2的面积分别成为S1、S2，且4S2-16S1=5π，求平移后所得抛物线的解析式；
（3）由（2）所得的抛物线与y轴交于点C，⊙O1和⊙O2的一条外公切线MN分别交x轴和y轴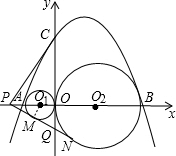
于点P、Q（M、N为切点，如图所示），求△CPQ的面积．
查看习题详情和答案>>
（1）请问：⊙O1和⊙O2，能否为等圆？若能，求出其半径的长度；若不能，说明理由；
（2）设抛物线向上平移4个单位后，⊙O1、⊙O2的面积分别成为S1、S2，且4S2-16S1=5π，求平移后所得抛物线的解析式；
（3）由（2）所得的抛物线与y轴交于点C，⊙O1和⊙O2的一条外公切线MN分别交x轴和y轴
于点P、Q（M、N为切点，如图所示），求△CPQ的面积．
查看习题详情和答案>>
已知抛物线C1：y=-x2+2mx+n（m，n为常数，且m≠0，n＞0）的顶点为A，与y轴交于点C；抛物线C2与抛物线C1关于y轴对称，其顶点为B，连接AC，BC，AB．
注：抛物线y=ax2+bx+c（a≠0）的顶点坐标为(-
，
)．
（1）请在横线上直接写出抛物线C2的解析式： ；
（2）当m=1时，判定△ABC的形状，并说明理由；
（3）抛物线C1上是否存在点P，使得四边形ABCP为菱形？如果存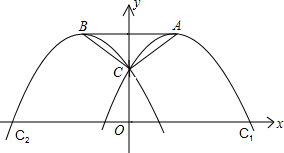
在，请求出m的值；如果不存在，请说明理由．
查看习题详情和答案>>
注：抛物线y=ax2+bx+c（a≠0）的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
（1）请在横线上直接写出抛物线C2的解析式：
（2）当m=1时，判定△ABC的形状，并说明理由；
（3）抛物线C1上是否存在点P，使得四边形ABCP为菱形？如果存
在，请求出m的值；如果不存在，请说明理由．
查看习题详情和答案>>
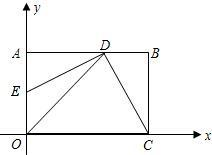已知：如图，在平面直角坐标系xOy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=2，OC=3．过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E．（1）求过点E、D、C的抛物线的解析式；
（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC交于点G．如果DF与（1）中的抛物线交于另一点M，点M的横坐标为
| 6 | 5 |
（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由． 查看习题详情和答案>>
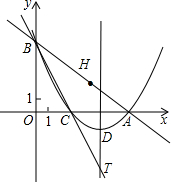将∠OBA对折，使点O的对应点H落在直线AB上，折痕交x轴于点C．