摘要:23.“伽利略 号木星探测器.从1989年10月进入太空起.历经6年.行程37亿千米.终于到达木星周围.此后在t秒内绕木星运行N圈后.对木星及其卫星进行考察.最后坠入木星大气层烧毁.设这N圈都是绕木星在同一个圆周上运行.其运行速率为v.探测器上的照相机正对木星拍摄到整个木星时的视角为θ.设木星为一球体.求: (1)木星探测器在上述圆形轨道上运行时的轨道半径, (2)若人类能在木星表面着陆.至少以多大的速度将物体从其表面水平抛出.才不至于使物体再落回木星表面.
网址:http://m.1010jiajiao.com/timu_id_4331489[举报]
本题满分16分)两个数列{an},{bn},满足bn=
.★(参考公式1+22+32+…+n2=
)
求证:{bn}为等差数列的充要条件是{an}为等差数列.
查看习题详情和答案>>
| a1+2a2+3a3+…+nan |
| 1+2+3+…+n |
| n(n+1)(2n+1) |
| 6 |
求证:{bn}为等差数列的充要条件是{an}为等差数列.
甲、乙两位同学都参加了由学校举办的篮球比赛,它们都参加了全部的7场比赛,平均得分均为16分,标准差分别为5.09和3.72,则甲、乙两同学在这次篮球比赛活动中,发挥得更稳定的是( )
查看习题详情和答案>>
(本题满分16分)已知点(1,![]() )是函数
)是函数![]() 且
且![]() )的图象上一点,等比数列
)的图象上一点,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]()
![]() 的首项为
的首项为![]() ,且前
,且前![]() 项和
项和![]() 满足
满足![]() -
-![]() =
=![]() +
+![]() (
(![]() ).
).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若数列{![]() 前
前![]() 项和为
项和为![]() ,问
,问![]() >
>![]() 的最小正整数
的最小正整数![]() 是多少? .
是多少? . ![]()
![]()
 (
(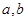 ∈R且
∈R且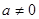 ),
),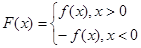 .
. ,且函数
,且函数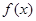 的值域为[0, +
的值域为[0, +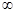 ),求
),求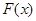 的解析式;
的解析式;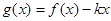 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;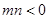 ,
,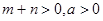 , 且
, 且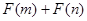 能否大于零?
能否大于零? 为等比数列,数列
为等比数列,数列 满足
满足 ,
, ,已知
,已知 ,
, ,其中
,其中 .
. 时,求
时,求 ;
; 为数列
为数列 项和,若对于任意的正整数
项和,若对于任意的正整数 ,求实数
,求实数 的取值范围.
的取值范围.