摘要:9. 如下图.已知△OFQ的面积为S.且·=1. (1)若<S<2.求向量与的夹角θ的取值范围, (2)设||=c(c≥2).S=c.若以O为中心.F为一个焦点的椭圆经过点Q.当||取最小值时.求椭圆的方程. 解:(1)由已知.得 ||||sin(π-θ)=S. ||||cosθ=1. ∴tanθ=2S. ∵<S<2.∴1<tanθ<4. 则<θ<arctan4. (2)以O为原点.所在直线为x轴建立平面直角坐标系. 设椭圆方程为+=1(a>b>0).Q(x.y). =(c.0).则=(x-c.y). ∵||·y=c.∴y=. 又∵·=c(x-c)=1.∴x=c+. 则||==(c≥2). 可以证明:当c≥2时.函数t=c+为增函数. ∴当c=2时. ||min==. 此时Q(.).将Q的坐标代入椭圆方程. 解得 得 +=1. a2=10. a2-b2=4. b2=6. ∴椭圆方程为+=1.
网址:http://m.1010jiajiao.com/timu_id_4067139[举报]
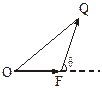
如下图,已知△OFQ的面积为S,且![]() ·
·![]() =1,
=1,
(1)若S的范围为![]() <S<2,求向量
<S<2,求向量![]() 与
与![]() 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设|![]() |=c(c≥2),S=
|=c(c≥2),S=![]() c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当|![]() |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
如下图,已知△OFQ的面积为S,且 ·
·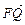 =1,
=1,
(1)若S的范围为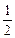 <S<2,求向量
<S<2,求向量 与
与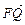 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设| |=c(c≥2),S=
|=c(c≥2),S= c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当|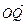 |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
 ·
·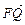 =1,
=1,
(1)若S的范围为
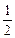 <S<2,求向量
<S<2,求向量 与
与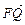 的夹角θ的取值范围;
的夹角θ的取值范围;(2)设|
 |=c(c≥2),S=
|=c(c≥2),S= c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当|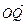 |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.

