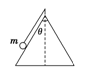
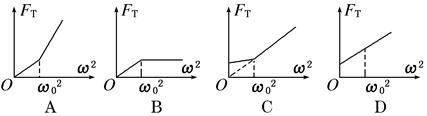
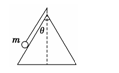
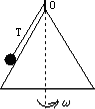
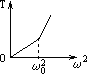
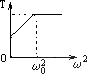
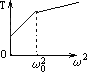
摘要:用一根细线一端系一小球.另一端固定在一光滑圆锥顶上. 如图4所示.设小球在水平面内做匀速圆周运动的角速度为ω.线的张力 为FT.则FT随ω2变化的图象是图5中的 ( ) 图4 图5 解析:小球角速度ω较小.未离开锥面时.设线的张力为FT.线的长度为L.锥面对小球的支持力为FN.则有FTcosθ+FNsinθ=mg.FTsinθ-FNcosθ=mω2Lsinθ.可得出:FT=mgcosθ+mω2Lsin2θ.可见随ω由0开始增加.FT由mgcosθ开始随ω2的增大.线性增大.当角速度增大到小球飘离锥面时.FT·sinα=mω2Lsinα.得FT=mω2L.可见FT随ω2的增大仍线性增大.但图线斜率增大了.综上所述.只有C正确. 答案:C
网址:http://m.1010jiajiao.com/timu_id_4063764[举报]
用一根细线一端系一小球(可视为质点),另一端固定在一光滑圆锥顶上, 如图4所示.设小球在水平面内做匀速圆周运动的角速度为ω,线的张力为FT,则FT随ω2变化的图象是图5中的 ( )


查看习题详情和答案>>
用一根细线一端系一小球(可视为质点),另 一端固定在一光滑锥顶上,如图所示,设小球在水平面内做匀速圆周运动的角速度为ω,细线的张力为FT,则FT随ω2变化的图象是

[ ]
A.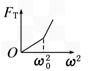
B.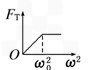
C.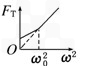
D.
查看习题详情和答案>>

B.
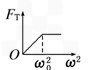
C.

D.

用一根细线一端系一小球(可视为质点),另一端固定在一光滑圆锥顶上, 如图4所示.设小球在水平面内做匀速圆周运动的角速度为ω,线的张力为FT,则FT随ω2变化的图象是图5中的 ( )