摘要:2. 说明:求导其本质是求极限.在求极限的过程中.力求使所求极限的结构形式转化为已知极限的形式.即导数的定义.这是能够顺利求导的关键.因此必须深刻理解导数的概念. 证明函数的在一点处连续 例 证明:若函数在点处可导.则函数在点处连续. 分析:从已知和要证明的问题中去寻求转化的方法和策略.要证明在点处连续.必须证明.由于函数在点处可导.因此.根据函数在点处可导的定义.逐步实现两个转化.一个是趋向的转化.另一个是形式的转化. 解:证法一:设.则当时.. ∴函数在点处连续. 证法二:∵函数在点处可导. ∴在点处有 ∴∴函数在点处连续. 说明:对于同一个问题.可以从不同角度去表述.关键是要透过现象看清问题的本质.正确运用转化思想来解决问题.函数在点处连续.有极限以及导数存在这三者之间的关系是:导数存在连续有极限.反之则不一定成立.证题过程中不能合理实现转化.而直接理解为是使论证推理出现失误的障碍.
网址:http://m.1010jiajiao.com/timu_id_4061931[举报]
A,B两人射击10次,命中环数如下:A:8 6 9 5 10 7 4 7 9 5; B:7 6 5 8 6 9 6 8 8 7
(1)求A,B 的平均数;
(2)求A,B两人的方差,并说明谁的射击成绩更好一些.
查看习题详情和答案>>
(1)求A,B 的平均数;
(2)求A,B两人的方差,并说明谁的射击成绩更好一些.
已知半径为 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(1)求圆的方程;
(2)设直线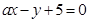
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看习题详情和答案>>