摘要:1求证: 证明:左边==右边 或:右边=tan(x-) ==左边 2若0<α<β<.sinα+cosα=.sinβ+cosβ=b.则 Aab<1 Ba>b Ca<b Dab>2 解:sinα+cosα=sin(α+)=a sinβ+cosβ=sin(β+)=b 又∵0<α<β< ∴0<α+<β+< ∴sin(α+)<sin(β+) ∴<b 答案:C
网址:http://m.1010jiajiao.com/timu_id_4058807[举报]
如图,已知曲线 ,曲线
,曲线 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与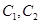 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.

(1)在正确证明 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线 与
与 有公共点,求证
有公共点,求证 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆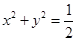 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
查看习题详情和答案>>
如图,已知曲线 ,曲线
,曲线 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.

(1)在正确证明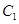 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线 与
与 有公共点,求证
有公共点,求证 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
查看习题详情和答案>>
 (2013•上海)如图,已知双曲线C1:
(2013•上海)如图,已知双曲线C1:| x2 |
| 2 |
(1)在正确证明C1的左焦点是“C1-C2型点“时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”;
(3)求证:圆x2+y2=
| 1 |
| 2 |
 已知圆O:
已知圆O: ,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
 内的点都不是“C1﹣C2型点”
内的点都不是“C1﹣C2型点”