摘要:已知椭圆上任意一点P.由P向x轴作垂线段PQ.垂足为Q.点M在线段PQ上.且=2.点M的轨迹为曲线E. (1)求曲线E的方程, 的直线l交曲线E于不同的两点G.H.且满足=2.求直线l的方程. 解 ,P(x0,y0), ∵=2.∴, 将其代入椭圆方程得 得曲线E的方程为:. (2)设G(x1.y1).H(x2.y2). ∵=2.∴x2=2x1. ① 依题意.当直线l斜率不存在时.G.不满足=2.故设直线l:y=kx+2,代入曲线E的方程并整理得(1+2k2)x2+8kx+6=0, ∴x1+x2=-,x1·x2= ② 联立①②解得k=±, 所以直线l的方程为:y=±x+2.
网址:http://m.1010jiajiao.com/timu_id_4058209[举报]
已知椭圆C的中心在坐标原点,焦点在坐标轴上,且过A(-2,0)、B(2,0)、C(1,
)三点.
(1)求椭圆C的方程;
(2)设点P是射线y=
x(x≥
)上(非端点)任意一点,由点P向椭圆C引两条切线PQ、PT(Q、T为切点),求证:直线QT的斜率为常数.
查看习题详情和答案>>
| ||
| 2 |
(1)求椭圆C的方程;
(2)设点P是射线y=
| 2 |
| 2 |
| 3 |
已知椭圆![]() =1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且
=1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且![]() =2
=2![]() ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)若过定点F(0,2)的直线l交曲线E于不同的两点G,H(点G在点F,H之间),且满足![]() =2
=2![]() ,求直线l的方程.
,求直线l的方程.
已知椭圆C的中心在坐标原点,焦点在坐标轴上,且过A(-2,0)、B(2,0)、C(1,
)三点.
(1)求椭圆C的方程;
(2)设点P是射线y=
x(x≥
)上(非端点)任意一点,由点P向椭圆C引两条切线PQ、PT(Q、T为切点),求证:直线QT的斜率为常数.
查看习题详情和答案>>
| ||
| 2 |
(1)求椭圆C的方程;
(2)设点P是射线y=
| 2 |
| 2 |
| 3 |
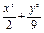 =1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且
=1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且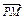 =2
=2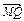 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.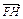 =2
=2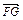 ,求直线l的方程.
,求直线l的方程.