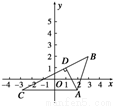
摘要:如图所示.已知点C的坐标是(2.2).过点C的直线CA与x轴交于点A.过点C且与直线CA垂直的直线CB与y轴交于点B.设点M是线段AB的中点.求点M的轨迹方程. 解 方法一 :设M的坐标为(x,y). 若直线CA与x轴垂直.则可得到M的坐标为(1.1). 若直线CA不与x轴垂直.设直线CA的斜率为k.则直线CB的斜率为-.故直线CA方程为:y=k(x-2)+2, 令y=0得x=2-,则A点坐标为(2-,0). CB的方程为:y=-(x-2)+2,令x=0,得y=2+. 则B点坐标为(0,2+).由中点坐标公式得M点的坐标为 ① 消去参数k得到x+y-2=0 , 点M(1.1)在直线x+y-2=0上. 综上所述.所求轨迹方程为x+y-2=0. 方法二 .依题意A点坐标为.∵|MA|=|MC|. ∴=, 化简得x+y-2=0. 方法三 依题意|MA|=|MC|=|MO|, 即:|MC|=|MO|,所以动点M是线段OC的中垂线.故由点斜式方程得到:x+y-2=0.
网址:http://m.1010jiajiao.com/timu_id_4058206[举报]


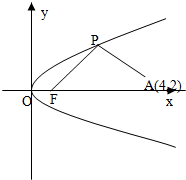 如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.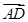 及点D的坐标.
及点D的坐标.