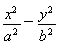摘要:9. 已知椭圆具有性质:若M.N是椭圆C上关于原点对称的两个点.点P是椭圆上任意一点.当直线PM.PN的斜率都存在.并记为kPM.kPN时.那么kPM与kPN之积是与点P位置无关的定值试对双曲线C′:-=1写出具有类似特性的性质.并加以证明 解:类似的性质为若MN是双曲线-=1上关于原点对称的两个点.点P是双曲线上任意一点.当直线PM.PN的斜率都存在.并记为kPM.kPN时.那么kPM与kPN之积是与点P位置无关的定值 设点M的坐标为(m.n). 则点N的坐标为(-m.-n). 其中-=1 又设点P的坐标为(x.y). 由kPM=.kPN=. 得kPM·kPN=·=. 将y2=x2-b2.n2=m2-b2.代入得 kPM·kPN= 点评:本题主要考查椭圆.双曲线的基本性质.考查类比.归纳.探索问题的能力它是一道综合椭圆和双曲线基本知识的综合性题目.对思维能力有较高的要求
网址:http://m.1010jiajiao.com/timu_id_4057188[举报]
已知椭圆具有性质:若M、N是椭圆C:
+
=1(a>b>0)上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线C′:
-
=1写出具有类似特性的性质,并加以证明.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,P是椭圆上任意一点,则当直线PM,PN的斜率都存在时,其乘积恒为定值.类比椭圆,写出双曲线C′:
-
=1(a>0,b>0)的类似性质,并加以证明.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线C′: 写出具有类似特性的性质,并加以证明.
查看习题详情和答案>>
写出具有类似特性的性质,并加以证明.
查看习题详情和答案>>
 =1写出具有类似特性的性质,并加以证明.
=1写出具有类似特性的性质,并加以证明.