摘要：21．设函数f2-ln(1+x)2. 的单调区间, (2)若当时.不等式f(x)<m恒成立.求实数m的取值范围, =x2+x+a在区间[0.2]上恰好有两个相异的实根.求实数a的取值范围. 本卷出题出发点:“发挥数学作为基础学科的作用.既重视考查中学数学基础知识的掌握程度.又注意考查进入高校继续学习的潜能 的要求.兼顾数学基础.方法.思维.应用和潜能等方面的考查.形成平稳发展的稳定格局.有利于高等学校选拔新生.有利于中学素质教育的实施.促进了数学教育改革的发展.突出对基础知识.基本技能.基本数学思想方法的考查.重视对数学基本能力和综合能力的考查.注重对数学应用意识和创新意识的考查. 本卷难度系数估计为:0.60--0.65
网址：http://m.1010jiajiao.com/timu_id_4052145[举报]
(本题满分14分) 设函数f (x)＝ln x＋
在 (0，
) 内有极值．
(Ⅰ) 求实数a的取值范围；
(Ⅱ) 若x1∈(0，1)，x2∈(1，＋
)．求证：f (x2)－f (x1)＞e＋2－．
注：e是自然对数的底数．
查看习题详情和答案>>
(本题满分14分) 设函数f (x)＝ln
x＋
在 (0，
) 内有极值．
(Ⅰ) 求实数a的取值范围；
(Ⅱ) 若x1∈(0，1)，x2∈(1，＋
)．求证：f (x2)－f (x1)＞e＋2－．
注：e是自然对数的底数．
查看习题详情和答案>>
(本题满分14分) 设函数f (x)＝ln x＋
在(0，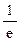
) 内有极值．
(Ⅰ) 求实数a的取值范围；
(Ⅱ) 若x1∈(0，1)，x2∈(1，＋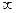
)．求证：f (x2)－f (x1)＞e＋2－．
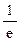注：e是自然对数的底数．
在(0，
) 内有极值．
)．求证：f (x2)－f (x1)＞e＋2－