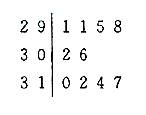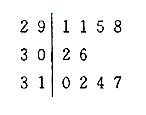摘要:3. 已知椭圆的中心在坐标原点.焦点在轴上.椭圆上的点到焦点距离的最大值为.最小值为. (Ⅰ)求椭圆的标准方程, (Ⅱ)若直线与椭圆相交于.两点(不是左右顶点).且以为直径的圆过椭圆的右顶点.求证:直线过定点.并求出该定点的坐标. [解析](Ⅰ)由已知易求出a.c的值.即得椭圆方程.(Ⅱ)由待定系数法设出直线方程.联立椭圆方程后由可以得到关于k和m的方程.求出满足的k和m的关系式后即可得到过定点的直线方程. [答案](I)由题意设椭圆的标准方程为 . (II)设.由得 . .. 以AB为直径的圆过椭圆的右顶点. .. . .解得 .且满足. 当时..直线过定点与已知矛盾, 当时..直线过定点 综上可知.直线过定点.定点坐标为
网址:http://m.1010jiajiao.com/timu_id_4051201[举报]
(08年山东卷理)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为
(A)304.6 (B)303.6 (C)302.6 (D)301.6