摘要:1 已知函数的图象与轴交点为.. 求证:. 证明:∵函数的图象与轴交点为. ∴+= =-1 ∴= ∴. 2 求证: 证明:∵ ∴ 3 求证: 证明:∵ ∴
网址:http://m.1010jiajiao.com/timu_id_4046753[举报]
已知函数f(x)=x3+ax2+bx+c
(Ⅰ)当b=1时,若函数f(x)在(0,1]上为增函数,求实数a的最小值;
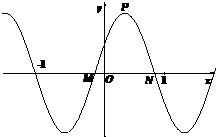
(Ⅱ)设函数f(x)的图象关于原点O对称,在点P(x0,f(x0))处的切线为l,l与函数f(x)的图象交于另一点Q(x1,y1).若P,Q在x轴上的射影分别为P1、Q1,
=λ
,求λ的值.
查看习题详情和答案>>
(Ⅰ)当b=1时,若函数f(x)在(0,1]上为增函数,求实数a的最小值;
(Ⅱ)设函数f(x)的图象关于原点O对称,在点P(x0,f(x0))处的切线为l,l与函数f(x)的图象交于另一点Q(x1,y1).若P,Q在x轴上的射影分别为P1、Q1,
| OQ1 |
| OP1 |
已知函数f(x)=x3+ax2+bx+c.
(Ⅰ)若a=-
,b=-6,c=1,求f(x)在[-2,4]上的最大值与最小值;
(Ⅱ)设函数f(x)的图象关于原点O对称,在点P(x0,f(x0))处的切线为l,l与函数f(x)的图象交于另一点Q(x1,y1).若P、Q在x轴上的射影分别为P1、Q1,
=λ
,求λ的值.
查看习题详情和答案>>
(Ⅰ)若a=-
| 3 |
| 2 |
(Ⅱ)设函数f(x)的图象关于原点O对称,在点P(x0,f(x0))处的切线为l,l与函数f(x)的图象交于另一点Q(x1,y1).若P、Q在x轴上的射影分别为P1、Q1,
| OQ1 |
| OP1 |
已知函数f(x)=ax2+bx+c,g(x)=ax+b
(1)令F(x)=
,当a、b、c满足什么条件时,F(x)为奇函数?
(2)令G(x)=f(x)-g(x),若a>b>c,且f(1)=0
(Ⅰ)求证函数G(x)的图象与x轴必有两个交点A、B;
(Ⅱ)求|AB|的取值范围. 查看习题详情和答案>>
(1)令F(x)=
| f(x) | g(x) |
(2)令G(x)=f(x)-g(x),若a>b>c,且f(1)=0
(Ⅰ)求证函数G(x)的图象与x轴必有两个交点A、B;
(Ⅱ)求|AB|的取值范围. 查看习题详情和答案>>
 已知函数
已知函数