摘要:已知a=,且∈. (1)求的最值, (2)若|ka+b|=|a-kb| ,求k的取值范围. 解 (1)a·b=-sin·sin+cos·cos=cos2. |a+b|2=|a|2+|b|2+2a·b=2+2cos2=4cos2. ∵∈.∴cos∈.∴|a+b|=2cos. ∴= =cos-. 令t=cos,则≤t≤1,′=1+>0, ∴t-在t∈上为增函数. ∴-≤t-≤. 即所求式子的最大值为.最小值为-. (2)由题设可得|ka+b|2=3|a-kb|2, ∴2=32 又|a|=|b|=1,a·b=cos2.∴cos2=. 由∈.得-≤cos2≤1. ∴-≤≤1.解得k∈[2-.2+]{-1}.
网址:http://m.1010jiajiao.com/timu_id_4046182[举报]
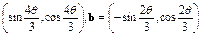 ,且
,且 ∈
∈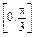 .
.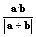 的最值;
的最值;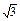 |a-kb| (k∈R),求k的取值范围.
|a-kb| (k∈R),求k的取值范围.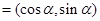 ,b
,b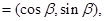 且a,b满足|ka+b |=
且a,b满足|ka+b |=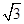 |a-kb|
|a-kb|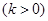 ,
,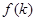 ;
;