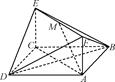
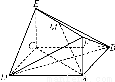
摘要:如图所示.已知正方形ABCD和矩形ACEF所在的平面互相垂直.AB=.AF=1.M是线段EF的中点. 求证: (1)AM∥平面BDE, (2)AM⊥平面BDF. 证明 (1)建立如图所示的空间直角坐标系, 设AC∩BD=N.连接NE. 则点N.E的坐标分别为.. ∴=. 又点A.M的坐标分别是 (..0).. ∴=. ∴=且NE与AM不共线.∴NE∥AM. 又∵NE平面BDE.AM平面BDE. ∴AM∥平面BDE. 知=. ∵D(.0.0).F(..1).∴=(0..1). ∴·=0.∴⊥. 同理⊥.又DF∩BF=F.∴AM⊥平面BDF.
网址:http://m.1010jiajiao.com/timu_id_4046170[举报]
 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,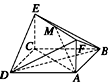
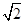 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.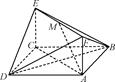
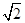 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.